某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件，若商场平均每天要盈利1200元，那么每件衬衫应降价多少元？

阅读下面的例题：

解方程：x²－|x|－2＝0

解：①当x≥0时，原方程化为x²－x－2＝0，解得x₁＝2，x₂＝－1(不合题意，舍去)；

②当x＜0时，原方程化为x²＋x－2＝0，解得：x₁＝1(不合题意，舍去)，x₂＝－2，所以原方程的解为x₁＝2，x₂＝－2．

请参照例题，解方程：x²－|x－1|－1＝0．

数学家高斯在上小学的时候，就曾快速地计算出了从1～100的连续整数的和，全体同学及老师无不惊叹万分，你知道高斯使用的方法吗？

现在同学们在计算这100个数字之和的时候，实际上也经常采用高斯求和法，即1＋2＋3＋…＋99＋100＝(1＋100)＋(2＋99)＋(3＋98)＋…＋(50＋51)＝101×50＝5050，另外，也还有类似的计算为：1＋2＋3＋…＋98＋99＋100①倒过来写：100＋99＋98＋…＋3＋2＋1　②

①＋②得1＋2＋3＋…＋98＋99＋100＝10100÷2＝5050．

以上两种作法，显然都可以理解为对称位置上放置了这些数字，含其中的1和100，2和99，3和98，…为对称数字，则对称数字之和均为101，继而得出结论5050，通过上述数学式子的解释，请观察下图方阵中的数字，试计算这25个数字的和．

如图所示，△与△ABC关于点O成中心对称，连结、、，分别交AC、于D、，你能说出图中一共有多少对形状和大小一样的三角形吗？每对三角形都是关于点O成中心对称吗？为什么？

如图所示，MN⊥PQ，垂足为O，A₁是A关于直线MN的对称点，A₂是A关于直线PQ的对称点，那么A₁，A₂的位置关系如何？写出你的结论并说明理由．

如图，在空间中，与定点的距离等于定长的点的集合叫做球面．定点叫做球心，定长叫做半径．球面被经过球心的平面截得的圆叫做大圆．

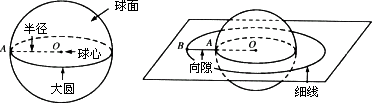
探究1：当我们把半径为11 cm的足球看成一个球时，假设有一根无弹性的细线恰好能沿足球的大圆紧紧缠绕一周，将细线的长度增加1米后，细线仍以圆形呈现，且圆心为足球的球心．若将细线与足球表面的间隙记为h₁(间隙如图所示)，求h₁的长；(π取3.14，结果精确到1 cm)

探究2：将探究1中的足球分别换成乒乓球和地球，其他条件都不改变．设乒乓球的半径为r，细线与乒乓球表面的间隙为h₂；地球的半径为R，细线与地球表面的间隙为h₃，试比较h₂与h₃的大小，并说明理由．

阅读下列材料：

如图表示我国农村居民的小康生活水平实现程度．

地处西部某贫困县，农村人口约50万，2002年农村小康生活的综合实现程度才达到68％，即没有达到小康程度的人口约为(1－68％)×50万＝16万．

解答下列问题：

(1)假设该县计划在2002年的基础上，到2004年底，使没有达到小康程度的16万农村人口降至10.24万，那么平均每年降低的百分率是多少？

(2)如果该计划实现，2004年底该县农村小康进程接近图中哪一年的水平？(假设该县人口2年内不变)

某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当降价措施，经调查发现如果每件衬衫每降价1元，商场平均每天可多售出2件，若商场平均每天要盈利1200元，每件衬衫应降价多少元．