如图，AB是半圆的直径，C为半圆上一点，CD⊥AB，F是上一点，AF交CD于点E．求证：AC²＝AE·AF．

如图所示，P为⊙O外一点，PB，PD分别交⊙O于A、B、C、D，PO平分∠BPD．

求证：∠AOB＝∠COD．

已知：如图所示，∠AOB＝90°，C、D是的三等分点，AB分别交OC、OD于点E、F．求证：AE＝BF＝CD．

已知：如图，AB是⊙O的直径，M是弦CD的中点，CE⊥AB于E，CD的延长线交AB的延长线于点P．

求证：PM·PC＝PO·PE．

如图：已知△ABC内接于⊙O，AD⊥BC，D为垂足，E为中点．求证：∠EAD＝∠EAO．

已知抛物线y＝ax²＋bx＋c过点A(－2，2)和B(2，－3)，求证关于x的二次方程ax²＋bx＋c＝0一定有两个不相等的实数根．

如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG．

(1)观察猜想BE与DG之间的大小关系，并正明你的结论；

(2)图中是否存在通过旋转能够互相重合的两个三角形？若存在，请说出旋转过程；若不存在，请说明理由．

已知：如图，AE²＝AD·AB，且∠1＝∠2，说明△BCE∽△EBD．

　　如图(1)，AB⊥BD，CD⊥BD，垂足分别为点B、D，AD与BC相交于点E，EF⊥BD，垂足为点F，则成立．

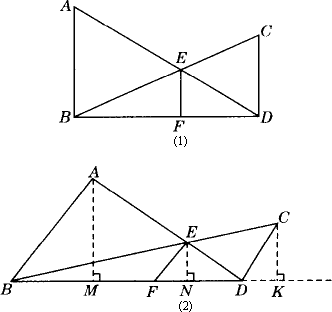
　　若将图中的垂直改为斜交如图(2)，AB∥CD，AD、BC相交于点F，过点E作EF∥AB，交BD于F，则(1)还成立吗？如果不成立，请说明理由；

(2)请找出S_△ABD、S_△BED与S_△BDC的关系，并给出证明．