如图所示，有一块形状是直角梯形的铁皮ABCD，它的上底AD=3cm，下底BC=8cm，垂直于底的腰CD=6cm．现在截出一块矩形铁皮MPCN，使它的顶点M、P、N分别在AB、BC、CD上．

(1)设MN为x，矩形MPCN的面积为S，求S关于x的函数解析式和x的取值范围．

(2)当MN的长是多少时，矩形MPCN的面积有最大值，这个值是多少？

启明公司生产某种产品，每件产品成本是3元，售价是4元，年销售量为10万件．为了获得更好的效益，公司准备拿出一定的资金作广告．根据经验，每年投入的广告费是x(万元)时，产品年销售量将是原销售量的y倍，且，如果把利润看作是销售总额减去成本费和广告费．

(1)试写出年利润s(万元)和广告费x(万元)的函数关系式，并计算广告费是多少万元时，公司获得的年利润最大，最大年利润是多少万元？

(2)把(1)中的最大利润留出3万元作广告，其余的资金投资新项目，现有6个项目可供选择，各项目每股投资金额和预计年收益如下表：

如果每个项目只能投一股，且要求所有投资项目的收益不得低于1.6万元，问有几种符合要求的投资方式？写出每种投资方式所选的项目．

某高科技发展公司投资500万元，成功研制出一种市场需求量较大的高科技替代产品，并投入资金1500万元进行批量生产．已知生产每件产品的成本为40元．在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件．设销售单价为x(元)，年销售量为y(万件)，年获利(年获利=年销售额－生产成本－投资)为z(万元)．

(1)试写出y与x之间的函数关系式(不必写出x的取值范围)．

(2)试写出z与x之间的函数关系式(不必写出x的取值范围)．

(3)计算销售单价为160元时的年获利，并说明同样的年获利，销售单价还可以定为多少元？相应的年销售量分别为多少万件？

(4)公司计划在第一年按年获利最大确定的销售单价进行销售；第二年年获利不低于1130万元．请你借助函数的大致图象说明，第二年的销售单价x(元)应确定在什么范围内?

已知抛物线y=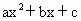开口向下，并且经过A(0，1)和M(2，－3)两点．

(1)若抛物线的对称轴为直线x=－1，求此抛物线的解析式．

(2)如果抛物线的对称轴在y轴的左侧，试求a的取值范围．

(3)如果抛物线与x轴交于B、C两点，且∠BAC=90°，求此时a的值．

已知函数y=的图象经过点(3，2)．

(1)求这个函数的解析式．

(2)画出它的图象，并指出图象的顶点坐标．

(3)当x＞0时，求使y≥2的x的取值范围．

炮弹的运行轨道若不计空气阻力是一条抛物线．现测得我军炮位A与射击目标B的水平距离为6000m，炮弹运行的最大高度为1200m．

(1)求此抛物的解析式．

(2)若A、B之间距离A点500m处有一高350m的障碍物，计算炮弹能否越过障碍物．

已知抛物线y=的开口向上，顶点P在直线y=－4x上，P点到坐标原点的距离为，抛物线与x轴的两个交点A、B的横坐标的平方和为10，求此抛物线的解析式．

已知二次函数y=．

(1)用配方法化为y=的形式．

(2)写出顶点A，图象与y轴交点B，与x轴交点C、D的坐标．

(3)画出草图．

(4)x为何值时，y随x的增大而增大．

(5)x为何值，y＞0、y=0、y＜0．

(6)求△BCD的面积．

求满足下列条件的对应的二次函数的关系式．

图象的顶点在(1，2)，过点(3，0)．

北京和上海都有某种仪器可供外地使用，其中北京可提供10台，上海可提供4台.已知重庆需要8台，武汉需要6台.从北京、上海将仪器运往重庆、武汉的费用如下表所示.有关部门计划用8000元运送这些仪器.请你设计一种方案，使武汉、重庆能得到所需的仪器,而且运费正好够用，又能否修改方案，降低整个运费？