(2007，湖北省黄冈市，21)张宇同学是一名天文爱好者，他通过查阅资料得知：地球、火星的运行轨道可以近似地看成是以太阳为圆心的两个同心圆，且这两个同心圆在同一平面上(如图所示)．由于地球和火星的运行速度不同，所以二者的位置不断发生变化．当地球、太阳和火星三者处在一条直线上，且太阳位于地球、火星中间时，称为“合”；当地球、太阳和火星三者处在一条直线上，且地球位于太阳与火星中间时，称为“冲”．另外，从地球上看火星与太阳，当两条视线互相垂直时，分别称为“东方照”和“西方照”．已知地球距太阳15(千万千米)，火星距太阳20.5(千万千米)．

(1)分别求“合”“冲”“东方照”“西方照”时，地球与火星的距离(结果保留准确值)．

(2)如果从地球上发射宇宙飞船登上火星，为了节省燃料，应选择在什么位置时发射较好？说明你的理由．

(注：从地球上看火星，火星在地球左、右两侧时分别叫做“东方照”“西方照”．)

(2005潍坊)如图，AD是ΔABC的角平分线，延长AD交于ΔABC的外接圆O于点E，过C、D、E三点的圆与AC的延长线交于点F，连结EF、DF．

(1)求证：△AEF∽ΔFED；

(2)若AD=6，DE=3，求EF的长；

(3)若DF∥BE，试判断ΔABE的形状，并说明理由．

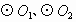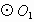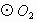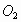(2005武汉)如图，已知：外切于点P，A是上一点，直线AC切于点C交于点B，直线AP交⊙于点D．

(1)请你判断∠BPC=∠CPD是否成立(不需证明)；

(2)将“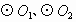外切于点P”改为“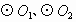内切于点P”，其他条件不变．(1)中的结论是否仍然成立？画出图形并证明你的结论．

(2006，黄冈)2005年10月，继杨利伟之后，航天员费俊龙、聂海胜又遨游了太空，这大大激发了王红庭同学爱好天文学的热情，他通过上网查阅资料了解到，金星和地球的运行轨道可以近似地看做以太阳为圆心的同心圆，且这两个同心圆在同一平面上(如图所示)，由于金星和地球的运转速度不同，所以二者的位置不断发生变化，当金星、地球距离最近时，此时叫“下合”；当金星、地球距离最远时，此时叫“上合”；在地球上观察金星的视线恰好与金星轨道相切时，此时分别叫“东大距”和“西大距”．已知地球与太阳相距约15千万千米，金星与太阳相距约10千万千米，分别求“下合”、“东大距”、“西大距”、“上合”时，金星与地球的距离(可用根号表示)．(注：在地球上观察金星，当金星分别在太阳的左、右两侧且视线恰好在与金星轨道相切的位置时，分别叫做西大距、东大距)

(2003　湖北武汉)如图a，已知、外切于点P，A是上一点，直线AC切于点C交于点B，直线AP交于点D．

(1)求证：PC平分∠BPD．

(2)将“、外切于点P”改为“、内切于点P”(见图b)，其他条件不变．(1)中的结论是否仍然成立？画出图形并证明你的结论．

(2003　重庆)如图所示：已知和相交于A、B两点，P是上一点，PB的延长线交于点C，PA交于点D，CD的延长线交于点N．

(1)过点A作AE∥CN交于点E，求证：PA=PE；

(2)连接PN，若PB=4，BC=2，求PN的长．

(2004　青海)如图所示，已知和外切于点A，直线BD切于点B，交于C、D，直线DA交于点E．

求证：(1)∠BAC=∠ABC＋∠D．

(2)连接BE，你还能推出哪些结论？(不再标注其他字母，不再添加辅助线，不写推理过程)写出五条结论即可．

(2007，内蒙古包头市，24)如图，已知AB是⊙O的直径，AC为弦，且平分∠BAD，AD⊥CD，垂足为D．

(1)求证：CD是⊙O的切线；

(2)若⊙O的直径为4，AD=3，试求∠BAC的度数．

(2007，甘肃省六市，24)如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C．若AB是⊙O的直径，D是BC的中点．

(1)试判断AB、AC之间的大小关系，并给出证明；

(2)在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点？(直接写出结论)

(2007，福建省厦门市，25)已知：如图，PA、PB是⊙O的切线，A、B是切点，连接OA、OB、OP，

(1)若∠AOP=60°，求∠OPB的度数；

(2)过O作OC、OD分别交AP、BP于C、D两点，

①若∠COP=∠DOP，求证：AC=BD；

②连接CD，设△PCD的周长为l，若l=2AP，判断直线CD与⊙O的位置关系，并说明理由．