已知，在Rt△OAB中，∠OAB＝90°，∠BOA＝30°，AB＝2．若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内．将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．

(1)求点C的坐标；

(2)若抛物线y＝ax²＋bx(a≠0)经过C、A两点，求此抛物线的解析式；

(3)若抛物线的对称轴与OB交于点D，点P为线段DB上一点，过P作y轴的平行线，交抛物线于点M．问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

注：抛物线y＝ax²＋bx＋c(a≠0)的顶点坐标为，对称轴公式为

我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售．按计划，20辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满．根据下表提供的信息，解答以下问题：

(1)设装运A种脐橙的车辆数为x，装运B种脐橙的车辆数为y，求y与x之间的函数关系式；

(2)如果装运每种脐橙的车辆数都不少于4辆，那么车辆的安排方案有几种？并写出每种安排方案；

(3)若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值．

在直角梯形ABCD中，∠C＝90^o，高CD＝6 cm(如图1)．动点P，Q同时从点B出发，点P沿BA，AD，DC运动到点C停止，点Q沿BC运动到C点停止．两点运动时的速度都是l cm/s．而当点P到达点A时，点Q正好到达点C．设P，Q同时从点B出发，经过的时间为t(s)时，△BPQ的面积为y(cm²)(如图2)．分别以x，y为横、纵坐标建立直角坐标系，已知点P在AD边上从A到D运动时，y与t的函数图象是图3中的线段MN．

(1)分别求出梯形中BA，AD的长度；

(2)写出图3中M，N两点的坐标；

(3)分别写出点P在BA边上和DC边上运动时，y与t的函数关系式(注明自变量的取值范围)，并在放大了的图3中补全整个运动中y关于t的函数关系的大致图象．

如图，抛物线y＝x²－2x－3与x轴交A、B两点(A点在B点左侧)，直线l与抛物线交于A、C两点，其中C点的横坐标为2．

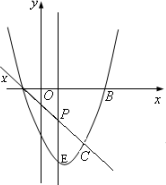
(1)求A、B两点的坐标及直线AC的函数表达式；

(2)P是线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值；

(3)点G抛物线上的动点，在x轴上是否存在点F，使A、C、F、G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由．

如图，某剧组在东海拍摄广泛风光片，拍摄基地位于A处，在其正南方向15海里处一小岛B，在B的正东方向20海里处有一小岛C，小岛D位于AC上，且距小岛A10海里．

(1)求∠A的度数(精确到1°)和点D到BC的距离；

(2)摄制组甲从A处乘甲船出发，沿A→B→C的方向匀速航行，摄制组乙从D处乘乙船出发，沿南偏西方向匀速直线航行，已知甲船的速度是乙船速度的2倍，若两船同时出发并且在B、C间的F处相遇，问相遇时乙船航行了多少海里？(结果精确到0.1海里)

如图，在平面直角坐标系中，坐标原点为O，A点坐标为(4，0)，B点坐标为(一1，0)，以AB的中点P为圆心，AB为直径作⊙P与y轴的正半轴交于点C．

(1)求经过A、B、C三点的抛物线对应的函数表达式．

(2)设M为(1)中抛物线的顶点，求直线MC对应的函数表达式．

(3)试说明直线MC与⊙P的位置关系，并证明你的结论．

某工厂生产的某种产品按质量分为10个档次．第1档次(最低档次)的产品一天能生产76件，每件利润10元．每提高一个档次，每件利润增加2元，但一天产量减少4件．

(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数，且1≤x≤10)，求出y关于x的函数关系式；

(2)若生产第x档次的产品一天的总利润为1080元，求该产品的质量档次．

如图所示，四边形ABDE内接⊙O，AE，BD的延长线相交于点C，直径AE为8，OC＝12，

(1)求证：；

(2)计算CD·CB的值，并指出CB的取值范围．

下表是七年级三班30名学生期末考试数学成绩表(已破损)已知该班学生期末考试数学成绩平均分是76分．

(1)求该班80分和90分的人数分别是多少？

(2)设该班30名学生成绩的众数为a，中位数为b，求a＋b的值．

　　数学课上，年轻的刘老师在讲授“轴对称”时，设计了如下四种教学方法：

　　①教师讲，学生听；

　　②教师让学生自己做；

　　③教师引导学生画图，发现规律；

　　④教师让学生对折纸，观察发现规律，然后画图．

　　数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中，要求每位同学选出自己最喜欢的一种，他随机抽取了60名学生的调查问卷，统计如图：

(1)请将条形统计图补充完整，并计算扇形统计图中方法③的圆心角．

(2)全年级同学中最喜欢的教学方法是哪一种？选择这种教学方法的约有多少人？

(3)假如抽取的60名学生集中在某两个班，这个调查结果还合理吗？为什么？

(4)请你对老师的教学方法提出一条合理化的建议．