如图，小方在五月一日假期中到郊外放风筝，风筝飞到C处时的线长为20米，此时小方正好站在A处，并测得∠CBD＝60°，牵引底端B离地面1.5米，求此时风筝离地面的高度(结果精确到个位)

解不等式组：；并把解集在数周上表示出来．

先化简，再求值：(1＋a)(1－a)＋a(a－2)，其中．

某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α(0°＜α＜90°)，如图(2)，AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

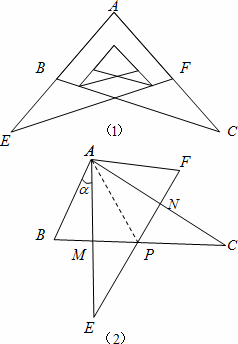
(1)求证：AM＝AN；

(2)当旋转角α＝30°时，四边形ABPE是什么样的特殊四边形？并说明理由．

为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

(1)求甲、乙两车单独运完此堆垃圾各需运多少趟？

(2)若单独租用一台车，租用哪台车合算？

2013年娄底市教育局对九年级学生的信息技术、物理实验操作、化学实验操作成绩进行抽样调查，成绩评定A、B、C、D四个等级．现抽取1000名学生成绩进行统计分析(其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级)，其相在数据统计如下：

(1)请将上表空缺补充完整；

(2)全市共有40000名学生参加测试，试估计该市九年级学生信息技术成绩合格以上(含合格)的人数；

(3)在这40000名学生中，化学实验操作达到优秀的大约有多少人？

2013年3月，某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象．已知A、B两点相距4米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度．(精确到0.1米，参考数据：≈1.41，≈1.73)

先化简，再求值：(x＋y)(x－y)－(4x³y－8xy³)÷2xy，其中x＝－1，．

如图，已知抛物线与x轴相交于A、B两点，与y轴相交于点C，若已知A点坐标为A(－2，0)．

(1)求抛物线的解析式及它的对称轴方程；

(2)求C点坐标，连接AC、BC并求线段BC所在直线的解析式；

(3)试判断△AOC与△COB是否相似？并说明理由；

(4)在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形，若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

如图，在平面直角坐标系xoy中，正比例函数y＝kx的图象与反比例函数y＝的图象有一个交点A(m，2)．

(1)求m的值；

(2)求正比例函数y＝kx的解析式；

(3)试判断点B(2，3)是否在正比例函数图象上，并说明理由．