在同一平面直角坐标系中有5个点：A(1，1)，B(－3，－1)，C(－3，1)，D(－2，－2)，E(0，－3)．

(1)画出△ABC的外接圆⊙P，并指出点D与⊙P的位置关系；

(2)若直线l经过点D(－2，－2)，E(0，－3)，判断直线l与⊙P的位置关系．

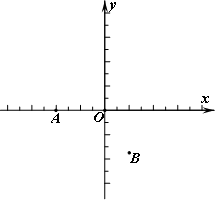
如图，在直角坐标系中，点A的坐标为(－2，0)，点B的坐标为，已知抛物线y＝ax²＋bx＋c(a≠0)经过三点A、B、O(O为原点)．

(1)求抛物线的解析式；

(2)在该抛物线的对称轴上，是否存在点C，使△BOC的周长最小．若存在，求出点C的坐标．若不存在，请说明理由；

(3)如果点P是该抛物线上x轴上方的一个动点，那么△PAB是否有最大面积．若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．(注意：本题中的结果均保留根号)．

如图，抛物线y₁＝x²－1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y₂，两条抛物线相交于点C．

(1)请直接写出抛物线y₂的解析式；

(2)若点P是x轴上一动点，且满足∠CPA＝∠OBA，求出所有满足条件的P点坐标；

(3)在第四象限内抛物线y₂上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．

如图，已知抛物线y＝ax²＋bx－2(a≠0)与x轴交于A、B两点，与y轴交于C点，直线BD交抛物线于点D，并且D(2，3)，tan∠DBA＝．

(1)求抛物线的解析式；

(2)已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值；

(3)在(2)中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线AC相切的圆，若存在，求出圆心Q的坐标，若不存在，请说明理由．

将两块全等的三角板如图①摆放，其中∠A₁CB₁＝∠ACB＝90°，∠A＝∠A＝30°．

(1)将图①中的△A₁B₁C顺时针旋转45°得图②，点P₁是A₁C与AB的交点，点Q是A₁B₁与BC的交点，求证：CP₁＝CQ；

(2)在图②中，若AP₁＝2，则CQ等于多少？

(3)如图③，在B₁C上取一点E，连接BE、P₁E，设BC＝1，当BE⊥P₁B时，求△P₁BE面积的最大值．

如图，在东西方向的海岸线l上有一长为1 km的码头MN，在码头西端M的正西19.5 km处有一观察站A，某时刻测得一艘匀速直线航行的轮船位于A处的北偏西30°且与A相距40 km的B处，经过1小时20分钟，又测得该轮船位于A处的北偏东60°且与A处相距8km的C处．

(1)求轮船航行的速度；(保留精确结果)

(2)如果该轮船不改变航向继续航行，那么轮船能否正好至码头MN靠岸？请说明理由．

如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB＝∠OBD＝30°，DB＝6cm．

(1)求证：AC是⊙O的切线；

(2)求由弦CD、BD与弧BC所围成的阴影部分的面积．(结果保留π)

如图，已知正方形ABCD的边长为4，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF＝45°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S₁．

(1)求证：∠APE＝∠CFP；

(2)设四边形CMPF的面积为S₂，CF＝x，y＝．

①求y关于x的函数解析式和自变量x的取值范围，并求出y的最大值；

②当图中两块阴影部分图形关于点P成中心对称时，求y的值．

下图①，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，，反比例函数在第一象限内的图象经过点A，与BC交于点F．

(1)若OA＝10，求反比例函数的解析式；

(2)若点F为BC的中点，且△AOF的面积S＝12，求OA的长和点C的坐标；

(3)在(2)的条件下，过点F作EF∥OB，交OA于点E(如图②)，点P为直线EF上的一个动点，连结PA，PO．是否存在这样的点P，使以P，O，A为顶点的三角形是直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．

如图1，点A是x轴正半轴上的动点，点B坐标为(0，4)，M是线段AB的中点，将点M绕点A顺时针方向旋转90°得到点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D点A关于直线CF的对称点，连结AC，BC，CD，设点A的横坐标为t

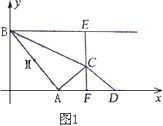
(1)当t＝2时，求CF的长；

(2)①当t为何值时，点C落在线段BD上？

②设△BCE的面积为S，求S与t之间的函数关系式；

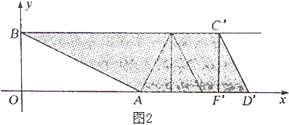
(3)如图2，当点C与点E重合时，△CDF沿x轴左右平移得到△，再将A，B，，为顶点的四边形沿剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形，请直接写出所有符合上述条件的点的坐标．