综合与探究：如图，抛物线与x轴交于A，B两点(点B在点A的右侧)与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为(m，0)，过点P作x轴的垂线l交抛物线于点Q

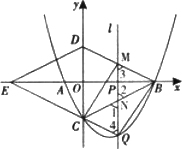
(1)求点A，B，C的坐标．

(2)当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．

(3)当点P在线段EB上运动时，是否存在点Q，使△BDQ为直角三角形，若存在，请直接写出点Q的坐标；若不存在，请说明理由．

问题情境：数学活动课上，老师出示了一个问题：

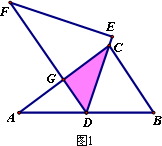
如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB＝∠E＝90°，BC＝DE＝6，AC＝FE＝8，顶点D与边AB的中点重合，DE经过点C，DF交AC于点G．求重叠部分(△DCG)的面积．

(1)独立思考：请解答老师提出的问题．

(2)合作交流：“希望”小组受此问题的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，你能求出重叠部分(△DGH)的面积吗？请写出解答过程．

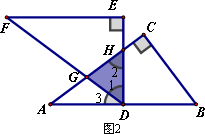
(3)提出问题：老师要求各小组向“希望”小组学习，将△DEF绕点D旋转，再提出一个求重叠部分面积的问题．“爱心”小组提出的问题是：如图3，将△DEF绕点D旋转，DE，DF分别交AC于点M，N，使DM＝MN求重叠部分(△DMN)的面积、

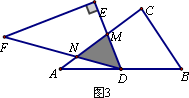
任务：①请解决“爱心”小组所提出的问题，直接写出△DMN的面积是________．

②请你仿照以上两个小组，大胆提出一个符合老师要求的问题，并在图中画出图形，标明字母，不必解答(注：也可在图(1)的基础上按顺时针方向旋转)．

通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．

原题：图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，连接EF，则EF＝BE＋DF，试说明理由．

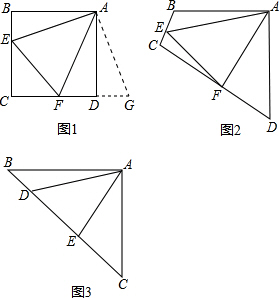
(1)思路梳理

∵AB＝CD，

∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．

∵∠ADC＝∠B＝90°，

∴∠FDG＝180°，点F、D、G共线．

根据________，易证△AFG≌________，得EF＝BE＋DF．

(2)类比引申

图2，四边形ABCD中，AB＝AD，∠BAD＝90°点E、F分别在边BC、CD上，∠EAF＝45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系________时，仍有EF＝BE＋DF．

(3)联想拓展

图3，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE＝45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

如图所示，已知直线y＝kx＋m与x轴、y轴分别交于A、C两点，抛物线y＝－x²＋bx＋c经过A、C两点，点B是抛物线与x轴的另一个交点，当时，y取最大值．

(1)求抛物线和直线的解析式；

(2)设点P是直线AC上一点，且S_△ABP：S_△BPC＝1∶3，求点P的坐标；

(3)若直线与(1)中所求的抛物线交于M、N两点，问：

①是否存在a的值，使得∠MON＝90°？若存在，求出a的值；若不存在，请说明理由；

②猜想当∠MON＞90°时，a的取值范围(不写过程，直接写结论)．

(参考公式：在平面直角坐标系中，若M(x₁，y₁)，N(x₂，y₂)，则M，N两点间的距离为)

如图(1)，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S₁、S₂，如果，那么称直线l为该图形的黄金分割线．

(1)如图(2)，在△ABC中，∠A＝36°，AB＝AC，∠C的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；

(2)若△ABC在(1)的条件下，如图(3)，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；

(3)如图(4)，在直角梯形ABCD中，∠D＝∠C＝90°，对角线AC、BD交于点F，延长AB、DC交于点E，连接EF交梯形上、下底于G、H两点，请问直线GH是不是直角梯形ABCD的黄金分割线，并证明你的结论．

已知关于x的二次函数y＝x²－2mx＋m²＋m的图象与关于x的函数y＝kx＋1的图象交于两点A(x₁，y₁)、B(x₂，y₂)；(x₁＜x₂)

(1)当k＝1，m＝0，1时，求AB的长；

(2)当k＝1，m为任何值时，猜想AB的长是否不变？并证明你的猜想．

(3)当m＝0，无论k为何值时，猜想△AOB的形状．证明你的猜想．

(平面内两点间的距离公式)．

如图(1)，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点(不与M、C重合)，以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．

(1)求证：OF∥BE；

(2)设BP＝x，AF＝y，求y关于x的函数解析式，并写出自变量x的取值范围；

(3)延长DC、FP交于点G，连接OE并延长交直线DC与H(图2)，问是否存在点P，使△EFO∽△EHG(E、F、O与E、H、G为对应点)，如果存在，试求(2)中x和y的值，如果不存在，请说明理由．

如图，点P是直线l：y＝-2x-2上的点，过点P的另一条直线m交抛物线y＝x²于A、B两点．

(1)若直线m的解析式为y＝-x+，求A、B两点的坐标；

(2)①若点P的坐标为(－2，t)，当PA＝AB时，请直接写出点A的坐标；

②试证明：对于直线l上任意给定的一点P，在抛物线上都能找到点A，使得PA＝AB成立．

(3)设直线l交y轴于点C，若△AOB的外心在边AB上，且∠BPC＝∠OCP，求点P的坐标．

科幻小说《实验室的故事》中，有这样一个情节，科学家把一种珍奇的植物分别放在不同温度的环境中，经过一天后，测试出这种植物高度的增长情况(如下表)：

由这些数据，科学家推测出植物每天高度增长量是温度的函数，且这种函数是反比例函数、一次函数和二次函数中的一种．

(1)请你选择一种适当的函数，求出它的函数关系式，并简要说明不选择另外两种函数的理由；

(2)温度为多少时，这种植物每天高度的增长量最大？

(3)如果实验室温度保持不变，在10天内要使该植物高度增长量的总和超过250 mm，那么实验室的温度应该在哪个范围内选择？请直接写出结果．

如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF＝90°，且EF交正方形外角的平分线CF于点F．

(1)图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE＝EF，请叙述你的一个构造方案，并指出是哪两个三角形全等(不要求证明)；

(2)如图2，若点E在线段BC上滑动(不与点B，C重合)．

①AE＝EF是否总成立？请给出证明；

②在如图所示的直角坐标系中，当点E滑动到某处时，点F恰好落在抛物线y＝－x²＋x＋1上，求此时点F的坐标．