
科目: 来源:北京市燕山区2010年初中毕业考试数学试卷 题型:059
如图,在直角坐标系中,O是坐标原点,点A的坐标是(1, ),若把线段OA绕点O逆时针旋转120°,可得线段OB.
),若把线段OA绕点O逆时针旋转120°,可得线段OB.

(1)求点B的坐标;
(2)某二次函数的图象经过A、O、B三点,求该函数的解析式;
(3)在第(2)小题所求函数图象的对称轴上,是否存在点P,使△OAP的周长最小,若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:北京市密云县2010年初中毕业考试数学试卷 题型:059
(1)观察与发现:
在一次数学课堂上,老师把三角形纸片ABC(AB>AC)沿过A点的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,
使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).有同学说此时的△AEF是等腰三角形,你同意吗?请说明理由.

(2)实践与运用
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点![]() 处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠α的大小是多少?(直接回答,不用说明理由).
处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠α的大小是多少?(直接回答,不用说明理由).

查看答案和解析>>
科目: 来源:北京市崇文区2010届初三第一次统一练习数学试卷 题型:059
正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=b(b<2a),且边AD和AE在同一直线上.小明发现:当b=a时,如图,在BA上选取中点G,连结FG和CG,裁掉△FAG和△CHD的位置构成正方形FGCH.

(1)类比小明的剪拼方法,请你就图①和图②两种情形分别画出剪拼成一个新正方形的示意图.

(2)要使(1)中所剪拼的新图形是正方形,须满足![]() =________.
=________.
查看答案和解析>>
科目: 来源:河北省石家庄市42中2010届初三毕业班第二次模拟考试数学试题 题型:059
两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为________和位置关系为________;

(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;

(2)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.

查看答案和解析>>
科目: 来源:北京市2006年高级中等学校招生统一考试(课标B卷)数学试卷 题型:059
如图,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.

请你参考这个作全等三角形的方法,解答下列问题:
(1)如图,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请你判断并写出FE与FD之间的数量关系;

(2)如图,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目: 来源:2006年湖南省郴州市课改实验区初中毕业学业考试试卷数学 题型:059
如下图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.

(1)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明.
(3)若D在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.
查看答案和解析>>
科目: 来源:2006年广东省广州市初中毕业生学业考试数学卷 题型:059
在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得到△AB1C1,使点C1落在直线BC上(点C1与点C不重合),
(1)如图,当∠C>60°,写出边AB1与边CB的位置关系,并加以证明;
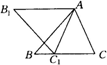
(2)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);
(3)当∠C<60°,请你在下图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否成立?并说明理由.
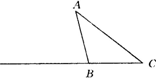
查看答案和解析>>
科目: 来源:2006年广东省梅州市初中毕业生学业考试数学试卷 题型:059
用两个全等的正方形ABCD和CDFE拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形ABEF的两边BE,EF相交于点G,H时,如图甲,通过观察或测量BG与EH的长度,你能得到什么结论?并证明你的结论.

(2)当直角三角尺的两直角边分别与BE的延长线,EF的延长线相交于点G,H时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.

查看答案和解析>>
科目: 来源:2006年浙江省金华市数学中考试题 题型:059
初三
(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:
请根据以上图案回答下列问题:
(1)
在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6 m,当AB为1 m,长方形框架ABCD的面积是________m2;(2)
在图案(2)中,如果铝合金材料总长度为6 m,设AB为1 m,长方形框架ABCD的面积为S=________(用含的代数式表示);当AB=________m时,长方形框架ABCD的面积S最大;在图案(3)中,如果铝合金材料总长度m,设AB为m,当AB=________m时,长方形框架ABCD的面积S最大.(3)
经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律.……探索:
如下面图案,如果铝合金材料总长度为
m共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.
查看答案和解析>>
科目: 来源:2006年山东省泰安市中等学校招生考试数学试卷(课改区) 题型:059
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=![]() ,∠BAO=30°.将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC.
,∠BAO=30°.将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC.

(1)求直线BC的解析式;
(2)求经过B,C,A三点的抛物线y=ax2+bx+c的解析式;若抛物线的顶点为M,试判断点M是否在直线BC上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com