已知二次函数当b取任何实数时，它的图象是一条抛物线．

(1)现在有如下两种说法：

①b取任何不同的数值时，所对应的抛物线都有着完全相同的形状；

②b取任何不同的数值时，所对应的抛物线都有着不相同的形状；你认为哪一种说法正确，为什么？

(2)若取b＝－1，b＝2时对应的抛物线的顶点分别为A、B，请你求出AB的解析式，并判断：当b取其它实数值时，所对应的抛物线的顶点是否在这条直线上？说明理由．

(3)在(2)中所确定的直线上有一点C且点C的纵坐标为－1，问在x轴上是否存在点D使△COD为等腰三角形，若存在直接写出点D坐标；若不存在，简单说明理由．

如图，AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直AB于点F，交BC于点G，连结PC，∠BAC＝∠BCP，求解下列问题：

(1)求证：CP是⊙O的切线．

(2)当∠ABC＝30°，BG＝，CG＝时，求以PD、PE的长为两根的一元二次方程．

(3)若(1)的条件不变，当点C在劣弧AD上运动时，应再具备什么条件可使结论BG²＝BF·BO成立？试写出你的猜想，并说明理由．

如图，已知AB是⊙O的直径，AC是⊙O的弦，点D是弧ABC中点，弦DE⊥AB，垂足为F，DE交AC于点G．

(1)图中有哪些相等的线段？(要求：不再标注其他字母，找结论的过程中所作的辅助线不能出现在结论中，不写出推理过程)

(2)若过点E作⊙O的切线ME，交AC的延长线于点M(请补完整图形)，试问：ME＝MG是否成立？若成立，请证明；若不成立，请说明理由．

(3)在满足第(2)问的条件下，已知AF＝3，FB＝，求AG与GM的比[第(1)的结论可直接利用]

如图，在直角坐标系中，以点P(1，－1)圆心，2为半径作圆，交x轴于A，B两点，抛物线过点A，B且顶点C在⊙P上．

(1)求⊙P上劣弧AB的长；

(2)求抛物线的解析式；

(3)在抛物线上是否存在一点D，使线段OC和PD互相平分？若存在，求出点D的坐标，若不存在请说明理由．

把两个全等的直角三角板ABC和EFG叠放在一起，使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，其中∠B＝∠F＝30°，斜边AB和EF长均为4．

(1)当EG⊥AC于点K，GF⊥BC于点H时(如图①)，求GH：GK的值

(2)现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转，旋转角α满足条件：0°＜α＜30°(如图②)，EG交AC于点K，GF交BC于点H，GH：GK的值是否改变？证明你发现的结论；

(3)在②下，连接HK，在上述旋转过程中，设GH＝x，△GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；

(4)三角板EFG由图①所示的位置绕O点逆时针旋转一周，是否存在某位置使△BFG是等腰三角形，若存在，请直接写出相应的旋转角α(精确到0.1°)；若不存在，说明理由．

已知，如图，Rt△ABC中，∠B＝90°，∠A＝30°，BC＝6 cm．点O从A点出发，沿AB以每秒 cm的速度向B点方向运动，当点O运动了t秒(t＞0)时，以O点为圆心的圆与边AC相切于点D，与边AB相交于E、F两点．过E作EG⊥DE交射线BC于G．

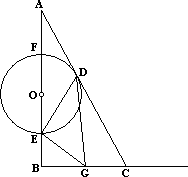
(1)若E与B不重合，问t为何值时，△BEG与△DEG相似？

(2)问：当t在什么范围内时，点G在线段BC上？当t在什么范围内时，点G在线段BC的延长线上？

(3)当点G在线段BC上(不包括端点B、C)时，求四边形CDEG的面积S(cm²)关于时间t(秒)的函数关系式，并问点O运动了几秒种时，S取得最大值？最大值为多少？

如图，已知抛物线y＝2x²－4x＋m与x轴交于不同的两点A、B，其顶点是C，点D是抛物线的对称轴与x轴的交点．

(1)求实数m的取值范围；

(2)求顶点C的坐标和线段AB的长度(用含有m的式子表示)；

(3)若直线分别交x轴、y轴于点E、F，问△BDC与△EOF是否有可能全等，如果可能，请证明；如果不可能，请说明理由．

在平面直角坐标系中(单位长度：1 cm)，A、B两点的坐标分别为(－4，0)，(2，0)，点P从点A开始以2 cm/s的速度沿折线AOy运动，同时点Q从点B开始以1 cm/s的速度沿折线BOy运动．

⑴在运动开始后的每一时刻一定存在以点A、O、P为顶点的三角形和以点B、O、Q为顶点的三角形吗？如果存在，那么以点A、O、P为顶点的三角形和以点B、O、Q为顶点的三角形相似吗？以点A、O、P为顶点的三角形和以点B、O、Q为顶点的三角形会同时成为等腰直角三角形吗？请分别说明理由．

⑵试判断时，以点A为圆心，AP为半径的圆与以点B为圆心、BQ半径的圆的位置关系；除此之外⊙A与⊙B还有其他位置关系吗？如果有，请求出t的取值范围．

⑶请你选定某一时刻，求出经过三点A、B、P的抛物线的解析式．

已知：抛物线y＝ax²＋4ax＋t与x轴的一个交点为A(－1，0)．

⑴求抛物线与x轴的另一个交点B的坐标．

⑵点D是抛物线与y轴的交点，点C是抛物线上的一点，且以AB为一底的梯形ABCD的面积为9，求此抛物线的解析式．

⑶点E是第二象限内到x轴、y轴的距离的比为5∶2的点，如果点E在⑵中的抛物线上，且它与点A在此抛物线对称轴的同侧，问：在抛物线的对称轴上是否存在点P，使△APE的周长最小？若存在，求出点P的坐标；若不存在，请说明理由．

操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．

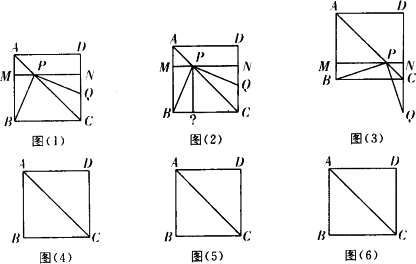
探究：设A、P两点间的距离为x．

⑴当点Q在CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到的结论(如图⑴)．

⑵当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域(如图⑵)．

⑶当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由(如图⑶)．(图⑷、图⑸、图⑹的的形状、大小相同，图⑷供操作、实验用，图⑸和图⑹备用)