如图，已知抛物线与x交于A(－1，0)、E(3，0)两点，与y轴交于点B(0，3)．

(1)求抛物线的解析式；

(2)设抛物线顶点为D，求四边形AEDB的面积；

(3)△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由．

如图，已知抛物线y＝x²＋bx＋c与坐标轴交于A、B、C三点，A点的坐标为(－1，0)，过点C的直线y＝x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．

(1)填空：点C的坐标是________，b＝________，c＝________；

(2)求线段QH的长(用含t的式子表示)；

(3)依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似？若存在，求出所有t的值；若不存在，说明理由．

在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，且点A(0，2)，点C(－1，0)，如图所示：抛物线y＝ax²＋ax－2经过点B．

(1)求点B的坐标；

(2)求抛物线的解析式；

(3)在抛物线上是否还存在点P(点B除外)，使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

如图，已知抛物线y＝x²＋4x＋3交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，点B的坐标为(－1，0)．

(1)求抛物线的对称轴及点A的坐标；

(2)在平面直角坐标系xoy中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；

(3)连结CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．

如图，已知直线，它与x轴、y轴的交点分别为A、B两点．

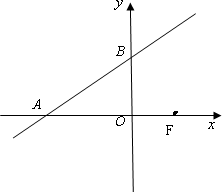
(1)求点A、点B的坐标；

(2)设F是x轴上一动点，用尺规作图作出⊙P，使⊙P经过点B且与x轴相切于点F(不写作法和证明，保留作图痕迹)；

(3)设(2)中所作的⊙P的圆心坐标为P(x，y)，求y与x的函数关系式；

(4)是否存在这样的⊙P，既与x轴相切又与直线l相切于点B，若存在，求出圆心P的坐标；若不存在，请说明理由．

已知矩形纸片OABC的长为4，宽为3，以长OA所在的直线为x轴，O为坐标原点建立平面直角坐标系；点P是OA边上的动点(与点O、A不重合)，现将△POC沿PC翻折得到△PEC，再在AB边上选取适当的点D，将△PAD沿PD翻折，得到△PFD，使得直线PE、PF重合．

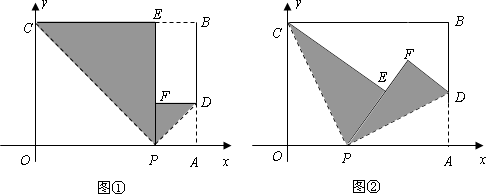
(1)若点E落在BC边上，如图①，求点P、C、D的坐标，并求过此三点的抛物线的函数关系式；

(2)若点E落在矩形纸片OABC的内部，如图②，设OP＝x，AD＝y当x为何值时，y取得最大值？

(3)在(1)的情况下，过点P、C、D三点的抛物线上是否存在点Q，使△PDQ是以PD为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标

如图，已知直线L过点A(0，1)和B(1，0)，P是x轴正半轴上的动点，OP的垂直平分线交L于点Q，交x轴于点M．

(1)直接写出直线L的解析式；

(2)设OP＝t，△OPQ的面积为S，求S关于t的函数关系式；并求出当0＜t＜2时，S的最大值；

(3)直线L₁过点A且与x轴平行，问在L₁上是否存在点C，使得△CPQ是以Q为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．

如图，矩形ABCD中，AB＝5，AD＝3．点E是CD上的动点，以AE为直径的⊙O与AB交于点F，过点F作FG⊥BE于点G．

(1)当E是CD的中点时：

①tan∠EAB的值为________；

②证明：FG是⊙O的切线；

(2)试探究：BE能否与⊙O相切？若能，求出此时DE的长；若不能，请说明理由．

已知：如图，直线l：，经过点，一组抛物线的顶点B₁(1，y₁)，B₂(2，y₂)，B₃(3，y₃)，…，B_n(n，y_n)(n为正整数)依次是直线l上的点，这组抛物线与x轴正半轴的交点依次是：A₁(x₁，0)，A₂(x₂，0)，A₃(x₃，0)，…，A_n+1(x_n+1，0)(n为正整数)，设x₁＝d(0＜d＜1)．

(1)求b的值；

(2)求经过点A₁、B₁、A₂的抛物线的解析式(用含d的代数式表示)

(3)定义：若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形，则这种抛物线就称为：“美丽抛物线”．

探究：当d(0＜d＜1)的大小变化时，这组抛物线中是否存在美丽抛物线？若存在，请你求出相应的d的值．

在正方形ABCD中，点E是AD上一动点，MN⊥AB分别交AB，CD于M，N，连结BE交MN于点O，过O作OP⊥BE分别交AB，CD于P，Q．

探究：(1)如图，当点E在边AD上时，请你动手测量三条线段AE，MP，NQ的长度，猜测AE与MP＋NQ之间的数量关系，并证明你所猜测的结论；

探究：(2)如图，若点E在DA的延长线上时，AE，MP，NQ之间的数量关系又是怎样？请直接写出结论；

再探究：(3)如图，连结并延长BN交AD的延长线DG于H，若点E分别在线段DH和射线HG上时，请在下图中完成符合题意的图形，并判断AE，MP，NQ之间的数量关系又分别怎样？请直接写出结论．