已知，抛物线y＝ax²＋bx＋c过点A(－3，0)，B(1，0)，，此抛物线的顶点为D．

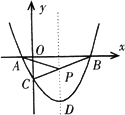
(1)求此抛物线的解析式；

(2)把△ABC绕AB的中点M旋转180°，得到四边形AEBC．

①求E点的坐标；

②试判断四边形AEBC的形状，并说明理由．

(3)试探求：在直线BC上是否存在一点P，使得△PAD的周长最小，若存在，请求出点P的坐标，若不存在，请说明理由．

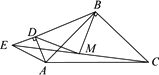
如图，已知点D在AC上，△ABC和△ADE都是等腰直角三角形，点M为EC的中点．

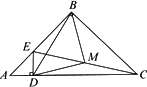
(1)求证：△BMD为等腰直角三角形

(2)将△ADE绕点A逆时针旋转45°，如图，(1)中的“△BMD为等腰直角三角形”是否仍然成立？请说明理由．

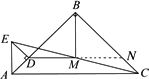
(3)将△ADE绕点A逆时针旋转135°，如图，(1)中的“△BMD为等腰直角三角形”成立吗？(不用说明理由)．

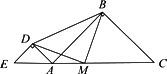
(4)我们是否可以猜想，将△ADE绕点A任意旋转一定的角度，如图，(1)中的“△BMD为等腰直角三角形”均成立？(不用说明理由)．

如图，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，则有结论EF＝BE＋FD成立；

(1)如图，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是BC、CD上的点，且∠EAF是∠BAD的一半，那么结论EF＝BE＋FD是否仍然成立？若成立，请证明；若不成立，请说明理由；

(2)若将(1)中的条件改为：在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，延长BC到点E，延长CD到点F，使得∠EAF仍然是∠BAD的一半，则结论EF＝BE＋FD是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．

如图，在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为(6，0)，点B的坐标为(4，3)，点C在y轴的正半轴上．动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t(秒)．

(1)求线段AB的长；当t为何值时，MN∥OC？

(2)设△CMN的面积为S，求S与t之间的函数解析式，并指出自变量t的取值范围；S是否有最小值？若有最小值，最小值是多少？

(3)连接AC，那么是否存在这样的t，使MN与AC互相垂直？若存在，求出这时的t值；若不存在，请说明理由．

如图，正方形ABCD的边长为，以O为原点建立平面直角坐标系，点A在x轴的负半轴上，点C在y轴的正半轴上，把正方形ABCO绕点O顺时针旋转α后得到正方形A₁B₁C₁O(α＜45°)，B₁C₁交y轴于点D，且D为B₁C₁的中点，抛物线y＝ax²＋bx＋c过点A₁，B₁，C₁．

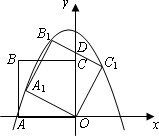
(1)求tanα的值；

(2)求点A₁的坐标，并直接写出点B₁、点C₁的坐标；

(3)求抛物线的函数表达式及其对称轴；

(4)在抛物线的对称轴上是否存在点P，使△PB₁C₁为直角三角形，若存在，直接写出所有满足条件的P点坐标；若不存在，请说明理由．

如图，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC＝PA，PD＝PB，∠APC＝∠BPD，连接CD，点E，F，G，H分别是AC，AB，BD，CD的中点，顺次连接E，F，G，H．

(1)猜想四边形EFGH的形状，直接回答，不必说明理由；

(2)当点P在线段AB的上方时，如图，在△APB的外部作△APC和△BPD，其它条件不变，(1)中结论还成立吗？说明理由；

(3)如果(2)中，∠APC＝∠BPD＝90°，其它条件不变，先补全图，再判断四边形EFGH的形状，并说明理由．

当x＝2时，抛物线y＝ax²＋bx＋c取得最小值－1，并且抛物线与y轴交于点C(0，3)，与x轴交于点A、B．

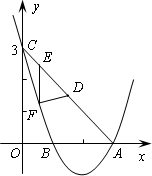
(1)求该抛物线的关系式；

(2)若点M(x，y₁)，N(x＋1，y₂)都在该抛物线上，试比较y₁与y₂的大小；

(3)D是线段AC的中点，E为线段AC上一动点(A、C两端点除外)，过点E作y轴的平行线EF与抛物线交于点F．问：是否存在△DEF与△AOC相似？若存在，求出点E的坐标；若不存在，则说明理由．

已知：Rt△ABC的斜边长为5，斜边上的高为2，将这个直角三角形放置在平面直角坐标系中，使其斜边AB与x轴重合(其中OA＜OB)，直角顶点C落在y轴正半轴上(如图)．

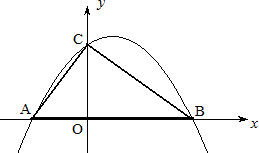
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式．

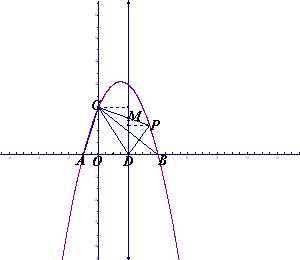
(2)如图，点D的坐标为(2，0)，点P(m，n)是该抛物线上的一个动点(其中m＞0，n＞0)，连接DP交BC于点E．

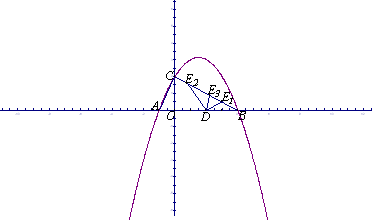
①当△BDE是等腰三角形时，直接写出此时点E的坐标．

②又连接CD、CP(如图)，△CDP是否有最大面积？若有，求出△CDP的最大面积和此时点P的坐标；若没有，请说明理由．

如图，二次函数y＝x²＋px＋q(p＜0)的图象与x轴交于A、B两点，与y轴交于点C(0，－1)，△ABC的面积为．

(1)求该二次函数的关系式；

(2)过y轴上的一点M(0，m)作y轴的垂线，若该垂线与△ABC的外接圆有公共点，求m的取值范围；

(3)在该二次函数的图象上是否存在点D，使四边形ACBD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由．

如图(1)，抛物线y＝x²－2x＋k与x轴交于A、B两点，与y轴交于点C(0，－3)．[图(2)、图(3)为解答备用图]

(1)k＝________，点A的坐标为________，点B的坐标为________；

(2)设抛物线y＝x²－2x＋k的顶点为M，求四边形ABMC的面积；

(3)在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；

(4)在抛物线y＝x²－2x＋k上求点Q，使△BCQ是以BC为直角边的直角三角形．