已知抛物线y＝x²―x―2．

(1)求抛物线顶点M的坐标；

(2)若抛物线与x轴的交点分别为点A、B(点A在点B的左边)，与y轴交于点C，点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时(点N不与点B，点M重合)，设NQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围；

(3)在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．

直线CD经过∠BCA的顶点C，CA＝CB．E、F分别是直线CD上两点，且∠BEC＝∠CFA＝∠α．

(1)若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面两个问题：

①如图，若∠BCA＝90°，∠α＝90°，则EF________|BE－AF|(填“＞”，“＜”或“＝”号)；

②如图，若0°＜∠BCA＜180°，若使①中的结论仍然成立，则∠α与∠BCA应满足的关系是________；

(2)如图，若直线CD经过∠BCA的外部，∠α＝∠BCA，请探究EF、与BE、AF三条线段的数量关系，并给予证明．

在图1中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE＝2b，且边AD和AE在同一直线上．

当2b＜a时，如图1，在BA上选取点G，使BG＝b，连结FG和CG，裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．

小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置，易知EH与AD在同一直线上．连结CH，由剪拼方法可得DH＝BG，故△CHD≌△CGB，从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置．这样，对于剪拼得到的四边形FGCH(如图1)，过点F作FM⊥AE于点M(图略)，利用SAS公理可判断△HFM≌△CHD，易得FH＝HC＝GC＝FG，∠FHC＝90°．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．

(1)正方形FGCH的面积是________；(用含a，b的式子表示)

(2)类比图1的剪拼方法，请你就图图4的三种情形分别画出剪拼成一个新正方形的示意图．

小明通过探究后发现：当b≤a时，此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．当b＞a时(如图)，能否剪拼成一个正方形？若能，请你在图中画出剪拼成的正方形的示意图；若不能，简要说明理由．

已知抛物线y＝ax²＋bx＋1经过点A(1，3)和点B(2，1)．

(1)求此抛物线解析式；

(2)点C、D分别是x轴和y轴上的动点，求四边形ABCD周长的最小值；

(3)过点B作x轴的垂线，垂足为E点．点P从抛物线的顶点出发，先沿抛物线的对称轴到达F点，再沿FE到达E点，若P点在对称轴上的运动速度是它在直线FE上运动速度的倍，试确定点F的位置，使得点P按照上述要求到达E点所用的时间最短．(要求：简述确定F点位置的方法，但不要求证明)

在△ABC中，∠ACB＝45°．点D(与点B、C不重合)为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．

(1)如果AB＝AC．如图，且点D在线段BC上运动．试判断线段CF与BD之间的位置关系，并证明你的结论．

(2)如果AB≠AC，如图，且点D在线段BC上运动．(1)中结论是否成立，为什么？

(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC＝，BC＝3，CD＝x，求线段CP的长．(用含x的式子表示)

如图，已知抛物线y＝ax²＋bx＋3(a≠0)与x轴交于点A(1，0)和点B(－3，0)，与y轴交于点C．

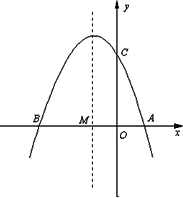
(1)求抛物线的解析式；

(2)点D的坐标为(－2，0)．问：直线AC上是否存在点F，使得△ODF是等腰三角形？若存在，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

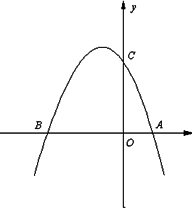
(3)如图，若点E为第二象限抛物线上一动点，连接BE、CE，求△BCE面积的最大值，并求此时E点的坐标．

如图①所示，在直角梯形ABCD中，∠BAD＝90°，E是直线AB上一点，过E作直线l∥BC，交直线CD于点F．将直线l向右平移，设平移距离BE为t(t≥0)，直角梯形ABCD被直线l扫过的面积(图中阴影部份)为S，S关于t的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．

(1)梯形上底的长AB＝________；

(2)直角梯形ABCD的面积＝________；

(3)写出图②中射线NQ表示的实际意义；

(4)当2＜t＜4时，求S关于t的函数关系式；

(5)当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1∶3．

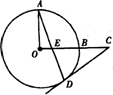
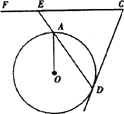
(1)如图，OA、OB是⊙O的半径，且OA⊥OB，点C是OB延长线上任意一点，过点C作CD切⊙O于点D，连结AD交DC于点E．则CD＝CE吗？如成立，试说明理由．

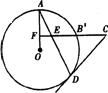
(2)若将图中的半径OB所在直线向上平行移动交OA于F，交⊙O于B’，其他条件不变，如图，那么上述结论CD＝CE还成立吗？为什么？

(3)若将图中的半径OB所在直线向上平行移动到⊙O外的CF，点E是DA的延长线与CF的交点，其他条件不变，如图，那么上述结论CD＝CE还成立吗？为什么．

如图，矩形是由矩形OABC(边OA在x轴正半轴上，边OC在y轴正半轴上)绕B点逆时针旋转得到的，点在x轴的正半轴上，B点的坐标为(1，3)．与AB交于D点．

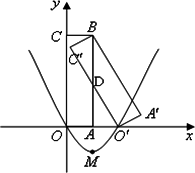
(1)求D点的坐标；

(2)如果二次函数y＝ax²＋bx＋c(a≠0)的图象经过点O、两点且图象顶点M的纵坐标为－1，求这个二次函数的解析式；

(3)若将直线OC绕点O旋转α度(0＜α＜90)后与抛物线的另一个交点为P，则以O、、B、P为顶点的四边形能否是平行四边形？若能，求出tanα的值；若不能，请说明理由．

已知：抛物线y＝ax²＋bx＋c(a≠0)的对称轴为x＝－1，与x轴交于A，B两点，与y轴交于点C，其中A(－3，0)、C(0，－2)．

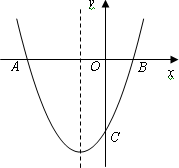
(1)求这条抛物线的函数表达式．

(2)已知在对称轴上存在一点P，使得△PBC的周长最小．请求出点P的坐标．

(3)若点D是线段OC上的一个动点(不与点O、点C重合)．过点D作DE∥PC交x轴于点E．连接PD、PE．设CD的长为m，△PDE的面积为S．求S与m之间的函数关系式．试说明S是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．