
科目: 来源:辽宁省辽阳市2011年初中毕业升学考试数学试卷 题型:059
已知直角梯形ABCD,AB∥CD,∠C=90°,AB=BC=![]() CD,E为CD的中点.
CD,E为CD的中点.
(1)如图(1)当点M在线段DE上时,以AM为腰作等腰直角三角形AMN,判断NE与MB的位置关系和数量关系,请直接写出你的结论;

(2)如图(2)当点M在线段EC上时,其他条件不变,(1)中的结论是否成立?请说明理由.

查看答案和解析>>
科目: 来源:辽宁省朝阳市2011年初中毕业升学考试数学试卷 题型:059
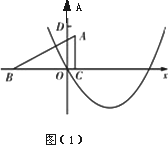
平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,-![]() );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(![]() ,0),且BC=5,AC=3(如图(1)).
,0),且BC=5,AC=3(如图(1)).
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图(1)、图(2)中画出探求);

②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:辽宁省朝阳市2011年初中毕业升学考试数学试卷 题型:059
如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,点D在AC上,点E在BC上,且CD=CE,连接DE.
,点D在AC上,点E在BC上,且CD=CE,连接DE.

(1)线段BE与AD的数量关系是________,位置关系是________.
(2)如图,当△CDE绕点C顺时针旋转一定角度α后,(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.

(3)绕点C继续顺时针旋转△CDE,当90°<α<180°时,延长DC交AB于点F,请在下图中补全图形,并求出当AF=1+![]() 时,旋转角α的度数.
时,旋转角α的度数.

查看答案和解析>>
科目: 来源:四川省资阳市2011年高中阶段教育学校招生考试数学试卷 题型:059
已知抛物线C:y=ax2+bx+c(a<0)过原点,与x轴的另一个交点为B(4,0),A为抛物线C的顶点.
(1)如图,若∠AOB=60°,求抛物线C的解析式;
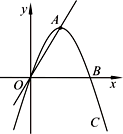
(2)如图,若直线OA的解析式为y=x,将抛物线C绕原点O旋转180°得到抛物线![]() ,求抛物线C、
,求抛物线C、![]() 的解析式;
的解析式;

(3)在(2)的条件下,设![]() 为抛物线
为抛物线![]() 的顶点,求抛物线C或
的顶点,求抛物线C或![]() 上使得PB=P
上使得PB=P![]() 的点P的坐标.
的点P的坐标.
查看答案和解析>>
科目: 来源:四川德阳市2011年初中毕业生学业考试与高中阶段学校招生考试数学试卷 题型:059
如图,已知抛物线经过原点O,与x轴交于另一点A,它的对称轴x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(m,-3),且与y轴、直线x=2分别交于点D,E.
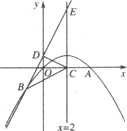
(1)求抛物线对应的函数解析式并用配方法把这个解析式化成y=a(x-h)2+k的形式;
(2)求证:CD⊥BE;
(3)在对称轴x=2上是否存在点P,使△PBE是直角三角形,如果存在,请求出点P的坐标,并求出△PAB的面积;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年辽宁省锦州市初中生学业考试数学试卷 题型:059
如图(1)~(3),已知∠AOB的平分线OM上有一点P,∠CPD的两边与射线OA、OB交于点C、D,连接CD交OP于点G,设∠AOB=α(0°<α<180°),∠CPD=β.
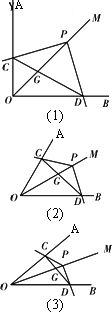
(1)如图(1),当α=β=90°时,试猜想PC与PD,∠PDC与∠AOB的数量关系(不用说明理由);
(2)如图(2),当α=60°,β=120°时,(1)中的两个猜想还成立吗?请说明理由.
(3)如图(3),当α+β=180°时,①你认为(1)中的两个猜想是否仍然成立,若成立请直接写出结论;若不成立,请说明理由.
②若![]() =2,求
=2,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源:广西贵港市2011年中考数学试题 题型:059
如图,已知直线y=-![]() x+2与抛物线y=a(x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
x+2与抛物线y=a(x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.

(1)请直接写出点A的坐标及该抛物线的解析式;
(2)若P为线段AB上一个动点(A、B两端点除外),连接PM,设线段PM的长为l,点P的横坐标为x,请求出l2与x之间的函数关系,并直接写出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在点P,使以A、M、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:内蒙古乌兰察布2011年中考数学试题 题型:059
如图,正比例函数和反比例函数的图象都经过点A(3,3),把直线OA向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y轴分别交于C、D两点.

(1)求m的值;
(2)求过A、B、D三点的抛物线的解析式;
(3)若点E是抛物线上的一个动点,是否存在点E,使四边形OECD的面积S1,是四边形OACD面积S的![]() ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年山东省青岛中考数学试题 题型:059
如图,在△ABC中,AB=AC=10 cm,BD⊥AC于点D,且BD=8 cm.点M从点A出发,沿AC的方向匀速运动,速度为2 cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1 cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为ts(0<t<5).

(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y cm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM=![]() S△ABC?若存在,求出t的值;若不存在,说明理由;
S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2011年山东省青岛中考数学试题 题型:059
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
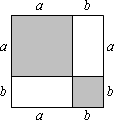
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类别应用
(1)已知小丽和小颖购买同一种商品的平均价格分别为![]() 元/千克和
元/千克和![]() 元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低.
元/千克(a、b是正数,且a≠b),试比较小丽和小颖所购买商品的平均价格的高低.
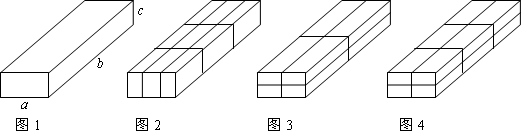
(2)试比较图1和图2中两个矩形周长M1、N1的大小(b>c).

联系拓广
小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图1所示(其中b>a>c>0),售货员分别可按图2、图3、图4三种方法进行捆绑,吻哪种方法用绳最短?哪种方法用绳最长?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com