
科目: 来源: 题型:解答题
种植草莓大户张华现有22吨草莓等售,现有两种销售渠道:一是运往省城直接批发给零售商;二是在本地市场零售.经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见下表:
| 销售渠道 | 每日销量(吨) | 每吨所获纯利润(元) |
| 省城批发 | 4 | 1200 |
| 本地零售 | 1 | 2000 |
查看答案和解析>>
科目: 来源: 题型:解答题
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,按原路原速返回,追上小明后两人一起步行到乙地.如图,线段OA表示小明与甲地的距离为y1(米)与行走的时间为x(分钟)之间的函数关系;折线BCDEA表示小亮与甲地的距离为y2(米)与行走的时间为x(分钟)之间的函数关系.请根据图像解答下列问题:
(1)小明步行的速度是 米/分钟,小亮骑自行车的速度 米/分钟;
(2)图中点F坐标是( , )、点E坐标是( , );
(3)求y1、y2与x之间的函数关系式;
(4)请直接写出小亮从乙地出发再回到乙地过程中,经过几分钟与小明相距300米? 
查看答案和解析>>
科目: 来源: 题型:解答题
如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足-(a-4)2≥0,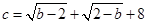
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求 的值
的值
查看答案和解析>>
科目: 来源: 题型:解答题
A城有肥料300吨,B城有肥料200吨,现要把这些肥料全部运往甲,乙两乡,从A城往甲,乙两乡运肥料的费用分别为每吨20元和25元;从B城往甲,乙两乡运肥料的费用分别为每吨25元和15元.现甲乡需要肥料260吨,乙乡需要肥料240吨.设从A城运往甲乡的肥料为x吨.
(1)请你填空完成下表中的每一空:
| 调入地 化肥量(吨) 调出地 | 甲乡 | 乙乡 | 总计 |
| A城 | x | _________ | 300 |
| B城 | _________ | _________ | 200 |
| 总计 | 260 | 240 | 500 |
查看答案和解析>>
科目: 来源: 题型:解答题
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息回答下列问题:
(1)甲乙两地的距离是 .
(2)到达乙地后卸货用的时间是 .
(3)这辆汽车返回的速度是 
查看答案和解析>>
科目: 来源: 题型:解答题
如图,一次函数 的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点C的坐标;
(2)在x轴上求一点P,使它到B、C两点的距离之和最小.
查看答案和解析>>
科目: 来源: 题型:解答题
科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系,经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米,在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)已知某山的海拔高度为1400米,请你求出该山山顶处的空气含氧量约为多少?
查看答案和解析>>
科目: 来源: 题型:解答题
图中折线是某个函数的图象,根据图象解答下列问题.
(1)写出自变量x的取值范围:____________,函数值y的取值范围:_____________.
(2)自变量x=1.5时,求函数值.
查看答案和解析>>
科目: 来源: 题型:解答题
如图①是一个长方形ABCD,点P按B→C→D→A方向运动,开始时,以每秒2个单位长度匀速运动,到达C点后,改为每秒a个单位匀速运动,到达D后,改为每秒b个单位匀速运动,在整个运动过程中,三角形ABP的面积S与运动时间t的函数关系如图所示。
求:
(1)AB、BC的长;
(2)a,b的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com