
科目: 来源: 题型:解答题
“节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如表所示:
| 价格种类 | 进价(元/台) | 售价(元/台) |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空调 | 2400 | 2700 |
查看答案和解析>>
科目: 来源: 题型:解答题
如图,直线y=- x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).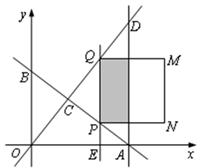
(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4,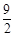 )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,已知反比例函数y1= (k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
查看答案和解析>>
科目: 来源: 题型:解答题
如图,一次函数y1=kx+b的图象与反比例函数y2= 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目: 来源: 题型:解答题
某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售),商品房售价方案如下:第八层售价为3 000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式.
(2)小张已筹到120 000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(3)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
查看答案和解析>>
科目: 来源: 题型:解答题
为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时(包括15吨),采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费,小兰家4、5月份的用水量及收费情况如下表:
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
查看答案和解析>>
科目: 来源: 题型:解答题
某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
查看答案和解析>>
科目: 来源: 题型:解答题
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com