如图，一次函数y=kx+b(k≠ 0)与反比例函数(m≠0)的图象有公共点A(1，2),D(a,-1)．直线 轴于点N(3，0)，与一次函数和反比例 函数的图象分别交于点B，C．

(1) 求一次函数与反比例函数的解析式；
(2) 求△ABC的面积。
(3) 根据图象回答，在什么范围时，一次函数的值大于反比例函数的值。

已知一次函数y=ｋx+ｂ的图象经过点A（０，－１），B（１，０），求这个一次函数的表达式．

如图所示，一次函数y=k₁x+b与反比例函数y=(x<0)的图象相交于A，B两点，且与坐标轴的交点为(–6,0)，(0,6)，点B的横坐标为–4．

（1）试确定反比例函数的解析式；
（2）求△AOB的面积；
（3）直接写出不等式k₁x+b>的解．

如图，梯形ABCD中，AB∥CD，AB=14，AD= 4，CD=7．直线l经过A，D两点，且sin∠DAB=．动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于AB，与折线A→D→C相交于点M，当P，Q两点中有一点到达终点时，另一点也随之停止运动．设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．

（1）求腰BC的长；
（2）当Q在BC上运动时，求S与t的函数关系式；
（3）在（2）的条件下，是否存在某一时刻t，使得△MPQ的面积S是梯形ABCD面积的？若存在，请求出t的值；若不存在，请说明理由；
（4）随着P，Q两点的运动，当点M在线段DC上运动时，设PM的延长线与直线l相交于点N，试探究：当t为何值时，△QMN为等腰三角形？

已知：如图，直线与x轴相交于点A，与直线相交于点P(2，)．

(1)请判断的形状并说明理由．
(2)动点E从原点O出发，以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合)，过点E分别作EF⊥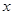轴于F，EB⊥轴于B．设运动t秒时，矩形EBOF与△OPA重叠部分的面积为S．
求：① S与t之间的函数关系式．
② 当t为何值时，S最大，并求S的最大值

如图①，一条笔直的公路上有A、B、C三地，B、C两地相距150千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地．甲、乙两车到A地的距离y₁、y₂（千米）与行驶时间x（时）的关系如图②所示．根据图象进行以下探究：


（1）请在图①中标出A地的位置，并作简要的文字说明；
（2）求图②中M点的坐标，并解释该点的实际意义；
（3）在图②中补全甲车的函数图象，求甲车到A地的距离y₁与行驶时间x的函数关系式；
（4）A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．

如图，在直角坐标系xOy中，直线与双曲线相交于、B两点，矩形的边恰好被点平分，边交双曲线于点，四边形的面积为2.

（1）求n的值；
（2）求不等式的解集

在同一直角坐标系中反比例函数y＝的图象与一次函数y＝kx＋b的图象相交，且其中一个交点A的坐标为（－2，3），若一次函数的图象又与x轴相交于点B，且△AOB的面积为6（点O为坐标原点）.求一次函数与反比例函数的解析式.

游泳池常需进行换水清洗，图中的折线表示的是游泳池换水清洗过程“排水——清洗——灌水”中水量y（m³）与时间t（min）之间的函数关系式.

（1）根据图中提供的信息，求整个换水清洗过程水量y（m³）与时间t（min）的函数解析式；
（2）问：排水、清洗、灌水各花多少时间？

如图，一次函数y₁＝kx＋b的图象与反比例函数y₂＝的图象相交于点A（2，3）和点B，与x轴相交于点C（8，0）.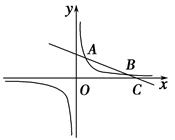

（1）求这两个函数的解析式；
（2）当x取何值时，y₁＞y₂.