
科目: 来源: 题型:解答题
我市化工园区一化工厂,组织20辆汽车装运A、B、C三种化学物资共200吨到某地.按计划20辆汽车都要装运,每辆汽车只能装运同一种物资且必须装满.请结合表中提供的信息,解答下列问题:
(1)设装运A种物资的车辆数为x,装运B种物资的车辆数为y.求y与x的函数关系式;
(2)如果装运A种物资的车辆数不少于5辆,装运B种物资的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?请求出最少总运费.
| 物资种类 | A | B | C |
| 每辆汽车运载量(吨) | 12 | 10 | 8 |
| 每吨所需运费(元/吨) | 240 | 320 | 200 |
查看答案和解析>>
科目: 来源: 题型:解答题
某文具店准备购进甲,乙两种钢笔,若购进甲种钢笔100支,乙种钢笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:解答题
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
查看答案和解析>>
科目: 来源: 题型:解答题
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
| 画板的边长(dm) | 10 | 20 |
| 出售价(元/张) | 160 | 220 |
查看答案和解析>>
科目: 来源: 题型:解答题
如图,一次函数y1=x+1的图象与反比例函数y2= (k为常数,且k≠0)的图象都经过点A(m,2).
(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1与y2的大小.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,已知反比例函数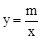 (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).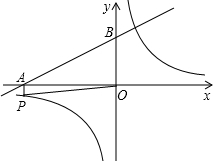
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO= (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
查看答案和解析>>
科目: 来源: 题型:解答题
如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使 与
与 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:解答题
如图:一次函数的图象与反比例函数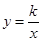 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)
(1)求反比例函数的解析式和B点坐标
(2)根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com