学习了函数的知识后，数学活动小组到文具店调研一种进价为每支2元的活动笔的销售情况。调查后发现，每支定价3元，每天能卖出100支，而且每支定价每下降0.1元，其销售量将增加10支。但是物价局规定，该活动笔每支的销售利润不能超过其进价的40%。设每支定价x元，每天的销售利润为y元。
（1）求每天的销售利润为y与每支定价x之间的函数关系式；
（2）如果要实现每天75元的销售利润，那么每支定价应为多少元？
（3）当每支定价为多少元时，可以使这种笔每天的销售利润最大？

某商家独家销售具有地方特色的某种商品，每件进价为40元．经过市场调查，一周的销售量y件与销售单价x（x≥50）元/件的关系如下表：

如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（-2，4），过点A作AB⊥y轴，垂足为B，连接OA．

（1）求△OAB的面积；
（2）若抛物线y=-x²-2x+c经过点A．
①求c的值；
②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）．

如图所示，在平面直角坐标系xOy中，矩形OABC的边长OA、OC分别为12cm、6cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax²+bx+c经过点A、B，且18a+c=0．

（1）求抛物线的解析式．
（2）如果点P由点A开始沿AB边以1cm/s的速度向终点B移动，同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动．
①移动开始后第t秒时，设△PBQ的面积为S，试写出S与t之间的函数关系式，并写出t的取值范围．
②当S取得最大值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由．

如图，在平面直角坐标系中，点A坐标为(-2，0)，点B坐标为（0，2），点E为线段AB上的动点(点E不与点A，B重合)，以E为顶点作∠OET=45°，射线ET交线段OB于点F，C为y轴正半轴上一点，且OC=AB，抛物线y=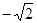x²+mx+n的图象经过A，C两点.

（1）求此抛物线的函数表达式；
（2）求证：∠BEF=∠AOE；
（3）当△EOF为等腰三角形时，求此时点E的坐标；
（4）在（3）的条件下，当直线EF交x轴于点D，P为（1）中抛物线上一动点，直线PE交x轴于点G，在直线EF上方的抛物线上是否存在一点P，使得△EPF的面积是△EDG面积的（）倍.若存在，请直接写出点P坐标；若不存在，请说明理由．

某公司开发了一种新型的家电产品，又适逢“家电下乡”的优惠政策．现投资40万元用于该产品的广告促销，已知该产品的本地销售量y₁（万台）与本地的广告费用x（万元）之间的函数关系满足，该产品的外地销售量y₂（万台）与外地广告费用t（万元）之间的函数关系可用如图所示的抛物线和线段AB来表示，其中点A为抛物线的顶点．

（1）结合图象，写出y₂（万台）与外地广告费用t（万元）之间的函数关系式；
（2）求该产品的销售总量y（万台）与外地广告费用t（万元）之间的函数关系式；
（3）如何安排广告费用才能使销售总量最大？

为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担，李明按照相关政策投资销售本市生产的一种新型节能灯，已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数：y=－10x＋500．
⑴李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
⑵设李明获得的利润为W(元)，当销售单价定为多少元时，每月可获得最大利润？
⑶物价部门规定，这种节能灯的销售单价不得高于25元，如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？

如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分C₁与经过点A、D、B的抛物线的一部分C₂组成一条封闭曲线，我们把这条封闭曲线称为“蛋线”，已知点C的坐标为（0，-），点M是抛物线C₂：y=mx²-2mx-3m(m<0)的顶点.

（1）求A、B两点的坐标；
（2）“蛋线”在第四象限内是否存在一点P，使得∆PBC的面积最大？若存在，求出∆PBC面积的最大值；若不存在，请说明理由；
（3）当∆BDM为直角三角形时，请直接写出m的值.(参考公式：在平面直角坐标系中，若M(x₁,y₁)，N(x₂,y₂)，则M、N两点间的距离为MN=.

如图，直线y=与x轴交于点A，与y轴交于点C，以AC为直径作⊙M，点是劣弧AO上一动点（点与不重合）．抛物线y=－经过点A、C，与x轴交于另一点B，

（1）求抛物线的解析式及点B的坐标；
（2）在抛物线的对称轴上是否存在一点P，是︱PA—PC︱的值最大；若存在，求出点P的坐标；若不存在，请说明理由。
（3）连交于点，延长至，使，试探究当点运动到何处时，直线与⊙M相切，并请说明理由．

如图(1)，直线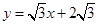与x轴交于点A、与y轴交于点D，以AD为腰，以x轴为底作等腰梯形ABCD(AB＞CD)，且等腰梯形的面积是8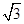，抛物线经过等腰梯形的四个顶点.

图(1)
(1) 求抛物线的解析式；
(2) 如图（2）若点P为BC上的—个动点（与B、C不重合），以P为圆心，BP长为半径作圆，与轴的另一个交点为E，作EF⊥AD，垂足为F，请判断EF与⊙P的位置关系，并给以证明；

图（2）
(3) 在（2）的条件下，是否存在点P，使⊙P与y轴相切，如果存在，请求出点P的坐标；如果不存在，请说明理由.