在平面直角坐标系中，矩形OABC过原点O，且A（0，2）、C（6，0），∠AOC的平分线交AB于点D．
（1）直接写出点B的坐标；
（2）如图，点P从点O出发，以每秒个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿轴正方向移动．设移动时间为秒．

①当t为何值时，△OPQ的面积等于1；
②当t为何值时，△PQB为直角三角形；
（3）已知过O、P、Q三点的抛物线解析式为y=-（x-t）²+t（t＞0）．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．

在二次函数中，函数y与自变量x的部分对应值如下表：

已知，二次函数的图像经过点和点B，其中点B在第一象限，且OA=OB，cot∠BAO=2．

（1）求点B的坐标；
（2）求二次函数的解析式；
（3）过点B作直线BC平行于x轴，直线BC与二次函数图像的另一个交点为C，联结AC，如果点P在x轴上，且△ABC和△PAB相似，求点P的坐标．

已知一个二次函数的图像经过点（4，1）和（，6）．
（1）求这个二次函数的解析式；
（2）求这个二次函数图像的顶点坐标和对称轴．

如图，已知抛物线与轴相交于A、B两点，与轴相交于点C，若已知B点的坐标为B（8，0）.

（1）求抛物线的解析式及其对称轴方程；
（2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由；
（3）M为抛物线上BC之间的一点，N为线段BC上的一点，若MN∥轴，求MN的最大值；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由.

已知一个二次函数的顶点A的坐标为（1，0），且图像经过点B（2，3）.
（1）求这个二次函数的解析式.
（2）设图像与y轴的交点为C，记，试用表示（直接写出答案）

为了改善市民的生活环境,我市在某河滨空地处修建一个如图所示的休闲文化广场．在Rt△内修建矩形水池,使顶点、在斜边上,、分别在直角边、上;又分别以、、为直径作半圆,它们交出两弯新月（图中阴影部分）,两弯新月部分栽植花草;其余空地铺设地砖．其中,．设米,米．

（1）求与之间的函数解析式;
（2）当为何值时,矩形的面积最大?最大面积是多少?
（3）求两弯新月（图中阴影部分）的面积,并求当为何值时,矩形的面积等于两弯新月面积的?

某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元．则每个月少卖10件(每件售价不能高于65元)．设每件商品的售价上涨元(为正整数),每个月的销售利润为元．
（1）求与的函数关系式并直接写出自变量的取值范围;
（2）每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
（3）每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?

已知抛物线经过点（3,0）,（－1,0）．
（1）求抛物线的解析式;
（2）求抛物线的顶点坐标．

如图,在平面直角坐标系中,已知点坐标为（2,4）,直线x=2与轴相交于点,连结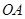,抛物线y=x从点沿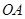方向平移,与直线x=2交于点,顶点到点时停止移动．

（1）求线段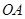所在直线的函数解析式;
（2）设抛物线顶点的横坐标为,
①用的代数式表示点的坐标;
②当为何值时,线段最短;
（3）当线段最短时,相应的抛物线上是否存在点,使△的面积与△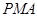的面积相等,若存在,请求出点的坐标;若不存在,请说明理由．