如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．

（1）求直线BD和抛物线的解析式．
（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．
（3）在抛物线上是否存在点P，使S_△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．

如图，直线AB分别交y轴、x 轴于A、B两点，OA=2，，抛物线过A、B两点.

（1）求直线AB和这个抛物线的解析式；
（2）设抛物线的顶点为D，求△ABD的面积
（3）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N.求当t 取何值时，MN的长度l有最大值？最大值是多少？

已知抛物线y＝ax²＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．

(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标，并求出此时的周长；
(3)在直线l上是否存在点M，使△MAC为直角三角形？若存在，请写出所有符合条件的点M的坐标；若不存在，请说明理由．

锐角△ABC中，BC=6，，两动点M,N分别在边AB,AC上滑动，且MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y(y＞0)．

(1)求△ABC中边BC上高AD；
(2)当x为何值时，PQ恰好落在边BC上（如图1）；
(3)当PQ在△ABC外部时（如图2），求y关于x的函数关系式（注明x的取值范围），并求出x为何值时y最大，最大值是多少？

某商品的进价为每千克40元，销售单价与月销售量的关系如下表（每千克售价不能高于65元）：

如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x(m)满足关系式y=a(x-6)²+2.6已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m.

（1）求y与x的关系式;（不要求写出自变量x的取值范围）
（2）球能否越过球网？球会不会出界？请说明理由；

如图，抛物线与x轴交于A（1，0）、B（﹣3，0）两点，与y轴交于点C（0，3），设抛物线的顶点为D．

（1）求该抛物线的解析式与顶点D的坐标．
（2）试判断△BCD的形状，并说明理由．
（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．

如图，直线与x轴、y轴分别交于点A、C，经过A、C两点的抛物线与x轴的负半轴上另一交点为B，且tan∠CBO=3．

（1）求该抛物线的解析式及抛物线的顶点D的坐标；
（2）若点P是射线BD上一点，且以点P、A、B为顶点的三角形与△ABC相似，求点P的坐标.

如图，抛物线与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．

（1）求抛物线的解析式，并求出点B坐标；
（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）
（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD相似？若存在请求出P点的坐标；若不存在，请说明理由．

鄞州区有一种可食用的野生菌，上市时，外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将以每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这类 野生菌在冷库中最多保存160天，同时，平均每天有3千克的野生菌损坏不能出售．
（1）设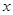天后每千克该野生菌的市场价格为y元，试写出y与x之间的函数关系式；
（2）若存放x天后，将这批野生菌一次性出售，设这批野生菌的销售总额为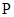元，试写出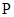与x之间的函数关系式；
（3）李经理将这批野生菌存放多少天后出售可获得最大利润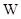元？
（利润＝销售总额－收购成本－各种费用）