某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．
（1）若商场平均每天要盈利1200元，每件衬衫应降价多少元？
（2）每件衬衫降价多少元，商场平均每天盈利最多？

为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．
（1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？

在平面直角坐标系xOy中，已知二次函数的图像经过原点及点A（1，2），与x轴相交于另一点B．

（1）求：二次函数的解析式及B点坐标；
（2）若将抛物线以为对称轴向右翻折后，得到一个新的二次函数，已知二次函数与x轴交于两点，其中右边的交点为C点．点P在线段OC上，从O点出发向C点运动，过P点作x轴的垂线，交直线AO于D点，以PD为边在PD的右侧作正方形PDEF（当P点运动时，点D．点E、点F也随之运动）；
①当点E在二次函数y₁的图像上时，求OP的长.
②若点P从O点出发向C点做匀速运动，速度为每秒1个单位长度，同时线段OC上另一个点Q从C点出发向O点做匀速运动，速度为每秒2个单位长度（当Q点到达O点时停止运动，P点也同时停止运动）.过Q点作x轴的垂线，与直线AC交于G点，以QG为边在QG的左侧作正方形QGMN（当Q点运动时，点G、点M、点N也随之运动），若P点运动t秒时，两个正方形分别有一条边恰好落在同一条直线上（正方形在x轴上的边除外），求此刻t的值.

如图，已知△ABC的三个顶点坐标分别为A（-4，0），B（1，0），C（-2，6）.

（1）求经过点A，B，C三点的抛物线解析式．
（2）设直线BC交y轴于点E，连结AE，求证：AE=CE；
（3）设抛物线与y轴交于点D，连结AD交BC于点F，求证：以A，B，F为顶点的三角形与△ABC相似，并求：．

某农户计划利用现有的一面墙（墙长8米），再修四面墙，建造如图所示的长方体水池，培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工，设图中与现有一面墙垂直的三面墙的长度都为xm，即AD＝EF＝BC＝xm.（不考虑墙的厚度）．

（1）若想水池的总容积为36m³，x应等于多少？
（2）求水池的总容积V与x的函数关系式，并直接写出x的取值范围；
（3）若想使水池的总容积V最大，x应为多少？最大容积是多少？

如图，抛物线与y轴交于点A，抛物线上的一点P在第四象限，连接AP与x轴交于点C，，且S_△AOC=1，过点P作PB⊥y轴于点B．

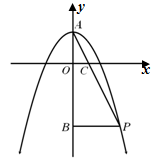
（1）求BP的长；
（2）求抛物线与x轴的交点坐标．

如图，在直角坐标系xOy中，二次函数y=x²+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．

（1）求这个二次函数的解析式；
（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；
（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由

某工厂生产某品牌的护眼灯，并将护眼灯按质量分成15个等级（等级越高，质量越好．如：二级产品好于一级产品）．若出售这批护眼灯，一级产品每台可获利21元，每提高一个等级每台可多获利润1元，工厂每天只能生产同一个等级的护眼灯，每个等级每天生产的台数如下表表示：

如图，直线交x轴于A点，交y轴于B点，抛物线经过点A、B，交x轴于另一点C，顶点为D．

（1）求抛物线的函数表达式；
（2）求点C、D两点的坐标；
（3）求△ABD的面积；

如图，黎叔叔想用60m长的篱笆靠墙MN围成一个矩形花圃ABCD，已知墙长MN=30m．

（1）能否使矩形花圃ABCD的面积为400m²？若能，请说明围法；若不能，请说明理由．
（2）请你帮助黎叔叔设计一种围法，使矩形花圃ABCD的面积最大，并求出最大面积．