
科目: 来源:不详 题型:单选题
| A.y3 | B.y2 |
| C.y1 | D.不能确定,与k的取值有关 |
查看答案和解析>>
科目: 来源:不详 题型:单选题
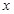 与函数值
与函数值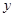 的对应值,判断方程ax2+b x+c=0(a≠0)的一个解
的对应值,判断方程ax2+b x+c=0(a≠0)的一个解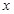 的范围是( )
的范围是( ) 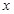 | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 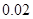 |  |
查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
科目: 来源:不详 题型:解答题
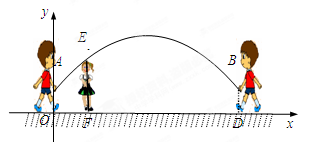
查看答案和解析>>
科目: 来源:不详 题型:解答题
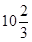 m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.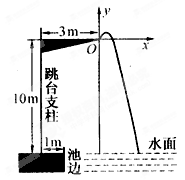
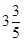 ,问:此次跳水会不会失误?通过计算说明理由.
,问:此次跳水会不会失误?通过计算说明理由.查看答案和解析>>
科目: 来源:不详 题型:解答题
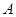 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与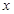 轴相交于点
轴相交于点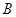 ,连结
,连结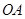 ,抛物线y=x
,抛物线y=x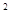
 从点
从点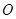 沿
沿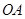 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点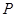 ,顶点
,顶点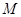 到
到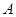 点时停止移动.
点时停止移动.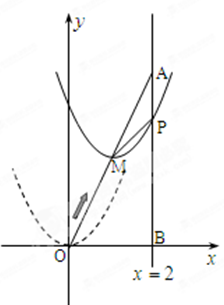
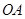 所在直线的函数解析式;
所在直线的函数解析式;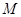 的横坐标为
的横坐标为 ,
, 的代数式表示点
的代数式表示点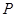 的坐标;
的坐标; 为何值时,线段
为何值时,线段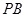 最短;
最短;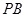 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△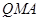 的面积与△
的面积与△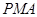 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com