
科目: 来源:不详 题型:解答题
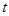 (月)之间的关系(即前
(月)之间的关系(即前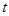 个月的利润总和S与
个月的利润总和S与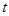 的关系).根据图象提供的信息,解答下列问题.
的关系).根据图象提供的信息,解答下列问题.
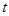 (月)之间的函数关系式;
(月)之间的函数关系式;查看答案和解析>>
科目: 来源:不详 题型:填空题
查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
 .请你计算这个“W”图案的高与宽的比到底是多少?
.请你计算这个“W”图案的高与宽的比到底是多少?查看答案和解析>>
科目: 来源:不详 题型:解答题

 的图象和性质.
的图象和性质.| x | … |  | 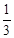 |  | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | … |

 的最小值.
的最小值.查看答案和解析>>
科目: 来源:不详 题型:解答题
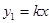 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数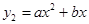 的图象如图②所示.
的图象如图②所示.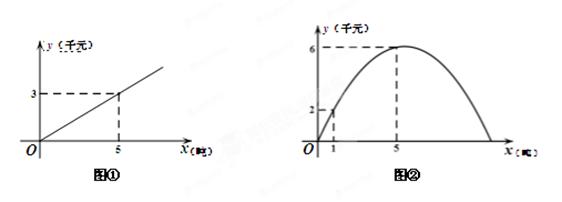
查看答案和解析>>
科目: 来源:不详 题型:填空题
| x | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -14 | -7 | -2 | 2 | m | n | -7 | -14 | -23 |
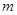 = ,
= ,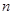 = .
= .查看答案和解析>>
科目: 来源:不详 题型:解答题
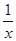 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+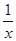 =2.
=2.查看答案和解析>>
科目: 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com