
科目: 来源:不详 题型:填空题
 是
是 边上一点,
边上一点, ⊥
⊥ 于点
于点 ,
, ⊥
⊥ 于点
于点 ,
, =
= ,∠
,∠ =∠
=∠ ,
, 与
与 相交于点
相交于点 ,下列结论:①
,下列结论:① ;②
;② ⊥
⊥ ;③
;③ ;④△
;④△ 的面积等于四边形
的面积等于四边形 的面积,其中正确的结论有
的面积,其中正确的结论有
查看答案和解析>>
科目: 来源:不详 题型:解答题
 ,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题:
,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题: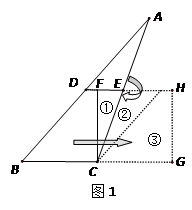
 .请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
.请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
查看答案和解析>>
科目: 来源:不详 题型:单选题

| A.逐渐增大 | B.逐渐减小 |
| C.始终不变 | D.先增大后变小 |
查看答案和解析>>
科目: 来源:不详 题型:解答题
 =BC.∴∠NMC=180°—∠AMN—∠
=BC.∴∠NMC=180°—∠AMN—∠ AMB=180°—∠B—∠AMB=∠MAB
AMB=180°—∠B—∠AMB=∠MAB
 MN是否还成立?请说明理由.
MN是否还成立?请说明理由.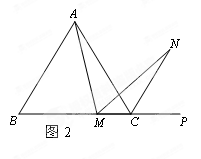
 边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)查看答案和解析>>
科目: 来源:不详 题型:单选题
 ABCD中,BC=7厘米,CD=5厘米,∠D=50°,
ABCD中,BC=7厘米,CD=5厘米,∠D=50°,
| A.∠C="130°" | B.∠BED=130° |
| C.AE=5厘米 | D.ED=2厘米 |
查看答案和解析>>
科目: 来源:不详 题型:填空题
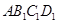 的边长为1,
的边长为1,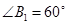 ;作
;作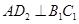 于点
于点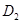 ,以
,以 为一边,做第二个菱形
为一边,做第二个菱形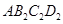 ,使
,使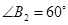 ;作
;作 于点
于点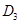 ,以
,以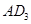 为一边做第三个菱形
为一边做第三个菱形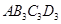 ,使
,使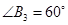 ;
; 依此类推,这样做的第
依此类推,这样做的第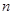 个菱形
个菱形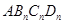 的边
的边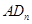 的长是_____________.x
的长是_____________.x
查看答案和解析>>
科目: 来源:不详 题型:解答题

查看答案和解析>>
科目: 来源:不详 题型:解答题


 如不能成功,请说明理由
如不能成功,请说明理由查看答案和解析>>
科目: 来源:不详 题型:解答题
 , ∠B=90°.
, ∠B=90°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com