如图，△ABC中，∠ACB=90°，∠B=30°，AD是角平分线，DE⊥AB于E，AD、CE相交于点H，则图中的等腰三角形有（　　）

A． 2个 B． 3个 C． 4个 D． 5个

如图，一个底角为70°的等腰三角形纸片，剪去顶角后，得到一个四边形，则∠1+∠2=　   　．

如图，△ABC中，∠C=90°，AD平分∠BAC交BC于点D，BD：DC=2：1，BC=7.8cm，则D到AB的距离为　  　cm．

如图，在△ABC中，AB=AC，D是底边BC的中点，作DE⊥AB于E，DF⊥AC于F
求证：DE=DF．
证明：∵AB=AC，∴∠B=∠C①．
在△BDE和△CDF中，∠B=∠C，∠BED=∠CFD，BD=CD，∴△BDE≌△CDF②．∴DE=DF③．
上面的证明过程是否正确？若正确，请写出①、②和③的推理根据．
（2）请你写出另一种证明此题的方法．

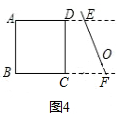
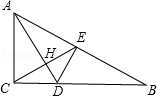
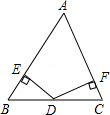
如图，在某小区的休闲广场有一个正方形花园ABCD，为了便于观赏，要在AD、BC之间修一条小路，在AB、DC之间修另一条小路，使这两条小路等长．设计师给出了以下几种设计方案：
①如图1，E是AD上一点，过A作BE的垂线，交BE于点O，交CD于点H，则线段AH、BE为等长的小路；

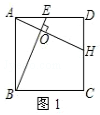
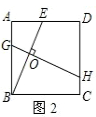
②如图2，E是AD上一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H，则线段GH、BE为等长的小路；

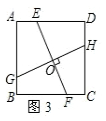
③如图3，过正方形ABCD内任意一点O作两条互相垂直的直线，分别交AD、BC于点E、F，交AB、CD于点G、H，则线段GH、EF为等长的小路；

根据以上设计方案，解答下列问题：
（1）你认为以上三种设计方案都符合要求吗？
（2）要根据图1完成证明，需要证明△　 　≌△　 　，进而得到线段　　=　　；
（3）如图4，在正方形ABCD外面已经有一条夹在直线AD、BC之间长为EF的小路，想在直线AB、DC之间修一条和EF等长的小路，并且使这条小路的延长线过EF上的点O，请画草图（加以论述），并给出详细的证明．

如图，∠A=50°∠ABC=60°．
（1）若BD为∠ABC平分线，求∠BDC．
（2）若CE为∠ACB平分线且交BD于E，求∠BEC．

如图，△ABC中，AB=AC，BD是AC边上的中线，BD把原三角形的周长分为15cm和9cm两部分，则腰AB的长为　  　cm．

如图，已知△ABC≌△CDA，∠BAC=60°，∠DAC=23°，则∠D=　  　．

已知△ABC的边长分别为a，b，c，化简|a+b﹣c|﹣|b﹣a﹣c|的结果是（　　）

A．2a

B．﹣2b

C．2a+3b

D．2b﹣2c

在各个内角都相等的多边形中，一个外角等于一个内角的，求这个多边形每一个内角的度数和它的边数．