
科目: 来源:2014中考名师推荐数学尺规作图(解析版) 题型:填空题
如图,在△ABC中,∠C=90°,∠A=30°,AB=2.按以下步骤作图:
①分别以点A和点B为圆心,以大于 AB的长为半径画弧,两弧相交于点M、N;
AB的长为半径画弧,两弧相交于点M、N;
②作直线MN,交AC于点D;
③连接BD.
则△BCD的周长为 .

查看答案和解析>>
科目: 来源:2014中考名师推荐数学尺规作图(解析版) 题型:解答题
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM. ②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.

查看答案和解析>>
科目: 来源:2014中考名师推荐数学尺规作图(解析版) 题型:解答题
如图,已知E是平行四边形ABCD对角线AC上的点,连接DE.
(1)过点B在平行四边形内部作射线BF交AC于点F,且使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接BE,DF,判断四边形BFDE的形状并证明.

查看答案和解析>>
科目: 来源:2014中考名师推荐数学展示定义、规则(解析版) 题型:解答题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,tanA= 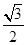 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求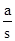 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
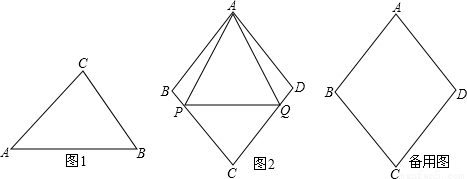
查看答案和解析>>
科目: 来源:2014中考名师推荐数学展示定义、规则(解析版) 题型:解答题
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣ ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.

查看答案和解析>>
科目: 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
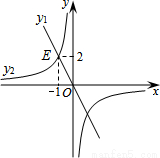
如图,正比例函数y1与反比例函数y2相交于点E(﹣1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是( )
A.
B.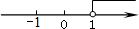
C.
D.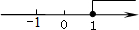
查看答案和解析>>
科目: 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中,正确的是( )

A.abc<0
B.a+c<b
C.b>2a
D.4a>2b﹣c
查看答案和解析>>
科目: 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y=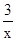 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )
A.0<x0<1
B.1<x0<2
C.2<x0<3
D.﹣1<x0<0
查看答案和解析>>
科目: 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:解答题
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)写出A、B两地之间的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.

查看答案和解析>>
科目: 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:解答题
已知a、b是正实数,那么,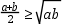 是恒成立的.
是恒成立的.
(1)由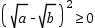 恒成立,说明
恒成立,说明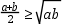 恒成立;
恒成立;
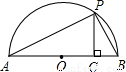
(2)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明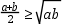 恒成立.
恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com