已知四边形ABCD顶点都在4×4的正方形网格格点上，如图所示，

（1）请画出四边形ABCD的外接圆，并标明圆心M的位置；

（2）这个圆中弦BC所对的圆周角的度数是 。

如图，矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.

（1）设Rt△CBD的面积为S1, Rt△BFC的面积为S2, Rt△DCE的面积为S3 , 则S1______ S2+ S3（用“>”、“=”、“<”填空）；

（2）写出图中的三对相似三角形，并选择其中一对进行证明。

如图，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE=4，CD=6，求AE的长。

某果园有100棵橙子树，每一棵树平均结600个橙子．现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。

（1）如果多种5棵橙子树，计算每棵橙子树的产量；

（2）如果果园橙子的总产量要达到60375个，考虑到既要成本低，又要保证树与树间的距离不能过密，那么应该多种多少棵橙子树？

（3）增种多少棵橙子树，可以使果园橙子的总产量最多？最多为多少？

如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动。小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径。

如图1，在平面直角坐标系中，O为坐标原点，P是反比例函数y=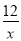（x＞0）图象上任意一点，以P为圆心，PO为半径的圆与坐标轴分别交于点A、B．

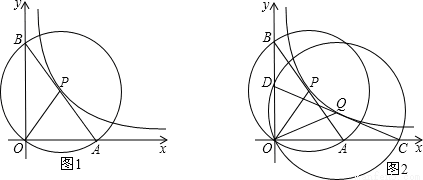
（1）求证：线段AB为⊙P的直径；

（2）求△AOB的面积；

（3）如图2，Q是反比例函数y=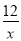（x＞0）图象上异于点P的另一点，以Q为圆心，QO为半径画圆与坐标轴分别交于点C、D．求证：DO•OC=BO•OA．

将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．

（1）如图①，对△ABC作变换[60°，]得△AB′C′，则S△AB′C′：S△ABC= ；直线BC与直线B′C′所夹的锐角为 度；

（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，BC=1,对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；

（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．

如图，在菱形ABCD中，AC、BD交于点O，AC=12cm，BD=16cm。动点P在线段AB上，由B向A运动，速度为1cm/s，动点Q在线段OD上，由D向O运动，速度为1cm/s。过点Q作直线EF┴BD交AD于E，交CD于F，连接PF，设运动时间为t（0<t<8）。问

（1）何时四边形APFD为平行四边形？求出相应t的值；

（2）设四边形APFE面积为ycm2，求y与t的函数关系式；.

（3）是否存在某一时刻t，使S四边形APFE:S菱形ABCD=17:40？若存在，求出相应t的值，并求出，P、E两点间的距离，若不存在，说明理由。

下列方程为一元二次方程的是

A．(a、b、c为常数)

B．

C．

D．

用配方法解方程时，原方程应变形为

A． B． C． D．