计算:(1)12-27+75 (2)(7+3)(7-3)-16 (3)-35+15+603．——青夏教育精英家教网—

相关习题

0 252592 252600 252606 252610 252616 252618 252622 252628 252630 252636 252642 252646 252648 252652 252658 252660 252666 252670 252672 252676 252678 252682 252684 252686 252687 252688 252690 252691 252692 252694 252696 252700 252702 252706 252708 252712 252718 252720 252726 252730 252732 252736 252742 252748 252750 252756 252760 252762 252768 252772 252778 252786 366461

科目： 来源： 题型：

计算：
（1）

（2）（

）（

）-

（3）-3

．

查看答案和解析>>

科目： 来源： 题型：

如图，在△ABC中，∠ABC=90°，AB=8cm，BC=6cm，点I在∠ABC和∠ACB的平分线上．ID⊥BC于点D，求ID的长．

查看答案和解析>>

科目： 来源： 题型：

关于x的一元二次方程x²-4x+5+m²=0的根的情况是（　　）

A、有两个不相等的实数根

B、有两个相等的实数根

C、没有实数根

D、根的情况不能确定

查看答案和解析>>

科目： 来源： 题型：

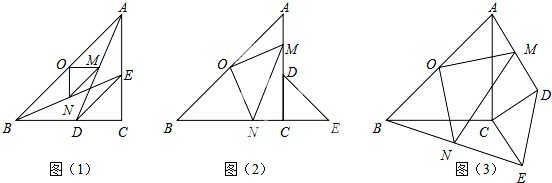
已知：在△ABC中，∠C=90°，BC=AC．
（1）如图（1），若点D、E分别在BC、AC边上，且CD=CE，连接AD、BE，点O、M、N分别是AB、AD、BE的中点．求证：△OMN是等腰直角三角形；
（2）将图（1）中△CDE绕着点C顺时针旋转90°如图（2），O、M、N分别为AB、AD、BE中点，则（1）中的结论是否成立，并说明理由；
（3）如图（3），若BC=AC=4，CD=CE=2，将图（1）中△CDE绕着点C顺时针旋转，记旋转角为α（0°＜a＜360°），O、M、N分别为AB、AD、BE中点，求在整个旋转过程中线段MN的最大值，并写出此时a的度数．