练习册

  • 练习册
  • 试题
    相关习题
     0  255842  255850  255856  255860  255866  255868  255872  255878  255880  255886  255892  255896  255898  255902  255908  255910  255916  255920  255922  255926  255928  255932  255934  255936  255937  255938  255940  255941  255942  255944  255946  255950  255952  255956  255958  255962  255968  255970  255976  255980  255982  255986  255992  255998  256000  256006  256010  256012  256018  256022  256028  256036  366461 

    科目： 来源： 题型：

    在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（-3，1），C（2，-2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．已知点A（1，2），B（-3，1），P（0，t）．
    （1）若A，B，P三点的“矩面积”为12，求点P的坐标；
    （2）直接写出A，B，P三点的“矩面积”的最小值．

    查看答案和解析>>

    科目： 来源： 题型：

    解下列各题
    （1）先化简，再求值：
    （m+n）2+（m+n）（m-3n）-（2m+n）（2m-n）-（-
    1
    2
    m2n）2；其中m=（-
    1
    2
    ）-1，n=-（π-3.1415）0；
    （2）已知方程组
    (m+1)x-(n-2)y=11
    mx+(n+3)y=7
    的一个解为
    x=-1
    y=-2
    ，求m，n的值；
    （3）分解因式-
    1
    4
    x3+x2y-xy2；
    （4）已知4x-x2-1=0，求代数式（2x-3）2-（x+y）（x-y）-y2的值．

    查看答案和解析>>

    科目： 来源： 题型：

    用白铁皮做盒子，每张铁皮可生产12个盒身或者18个盒盖，现有49张铁皮，怎样安排生产盒身和盒盖的铁皮张数，才能使生产的盒身与盒盖配套（一张铁皮只能生产一种产品，一个盒身配两个盒盖）？

    查看答案和解析>>

    科目： 来源： 题型：

    解下列不等式和不等式组并把它们的解集在数轴上表示出来：
    （1）
    1
    2
    x-1≤
    2
    3
    （2x+1）；
    （2）
    2x+3≤x+11(1)
    2x+5
    3
    -1＞2-x(2)
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    为了解某区九年级学生的视力情况，随机抽取了该区若干名九年级学生的视力等级进行了统计分析，并绘制了如下的统计图表（不完整）：
    视力等级ABCD
    人数9015

    请根据以上统计图表提供的信息，解答下列问题：
    （1）本次抽查的学生有
     
    名，等级为B类的学生人数为
     
    名，C类等级所在扇形的圆心角度数为
     
    ；
    （2）请补全条形统计图；
    （3）根据抽样调查结果，请估计该区约6000名九年级学生视力等级为D类的学生人数．

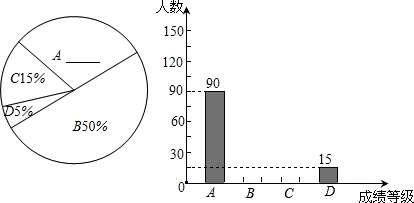
    查看答案和解析>>

    科目： 来源： 题型：

    种植草莓大户张华现有22吨草莓等售，现有两种销售渠道：一是运往省城直接批发给零售商；二是在本地市场零售．经过调查分析，这两种销售渠道每天销量及每吨所获纯利润见表：
    销售渠道每日销量（吨）每吨所获纯利润（元）
    省城批发41200
    本地零售12000
    受客观因素影响，每天只能采用一种销售渠道，草莓必须在10日内售出．
    （1）若一部分草莓运往省城批发给零售商，其余在本地市场零售，请写出销售22吨草莓所获纯利润y（元）与运往省城直接批发给零售商的草莓量x（吨）之间的函数关系式；
    （2）由于草莓必须在10日内售完，请你求出x的取值范围；
    （3）怎样安排这22吨草莓的销售渠道，才能使所获纯利润最大？并求出最大纯利润．

    查看答案和解析>>

    科目： 来源： 题型：

    判断A（1，3）、B（-2，0）、C（-4，-2）三点是否在同一直线上，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

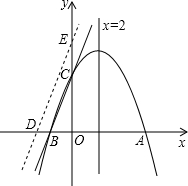    如图，对称轴为直线x=2的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中A点的坐标为（5，0）．
    （1）求点B的坐标；
    （2）已知a=-1，C为抛物线与y轴的交点．
    ①若点P在抛物线上，且S△POC=3S△BOC，求点P的坐标； 
    ②当直线BC左右平移时，直线与x轴、y轴分别交于D、E，对称轴上是否存在点M，使得△DEM为等腰直角三角形？若存在，直接写出点M的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，两座建筑物AB与CD，其水平距离BD为30米，在从AB的顶点A处用高1.2米的测角仪AE测得CD的顶部C的仰角α=30°，测得其底部D的俯角β=45°，求两座建筑物AB与CD的高．（精确到0.1米）

    查看答案和解析>>

    科目： 来源： 题型：

    如图，直线y=-x+5分别与x轴、y轴交于A、B两点．
    （1）求A、B两点的坐标；
    （2）已知点C坐标为（4，0），设点C关于直线AB的对称点为D，请直接写出点D的坐标；
    （3）请在直线AB和y轴上分别找一点M、N使△CMN的周长最短，在平面直角坐标系中作出图形，并求出点N的坐标．

    查看答案和解析>>

    同步练习册答案