
科目: 来源: 题型:

查看答案和解析>>
科目: 来源: 题型:
| 2 |
| ||
| 2 |
| EC-EA |
| EO |
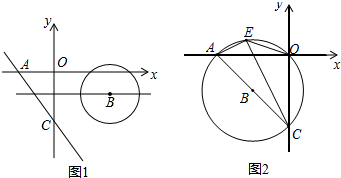
查看答案和解析>>
科目: 来源: 题型:
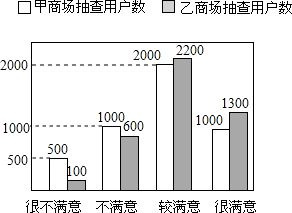 在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级.
在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级.查看答案和解析>>
科目: 来源: 题型:
| k |
| x |
| DO |
| EF |

查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
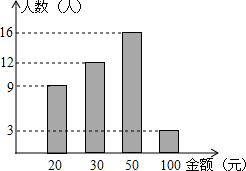 春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.
春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.查看答案和解析>>
科目: 来源: 题型:
 (1)在平面直角坐标系中画出下列各点:A(-2,-3)、D(0,2)
(1)在平面直角坐标系中画出下列各点:A(-2,-3)、D(0,2)查看答案和解析>>
科目: 来源: 题型:
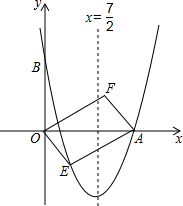 如图,对称轴为直线x=
如图,对称轴为直线x=| 7 |
| 2 |
查看答案和解析>>
科目: 来源: 题型:
| CE |
| BD |
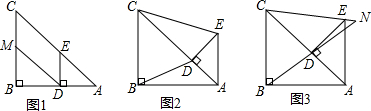
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com