已知抛物线m的顶点为M，抛物线m上部分点的横坐标与对应的纵坐标如下表：

x	…	-2	0	2	3	…
y	…	5	-3	-3	0	…

（1）根据表中的各对对应值，下列说法正确序号是．
①抛物线m开口向上；                        
②抛物线m的对称轴为x=1；
③抛物线m与x轴有一交点坐标为（-1，0）；
④当x=4时，对应的函数值y为5．
（2）若将抛物线m绕原点O顺时针旋转180°，试写出旋转后抛物线n的解析式，并在坐标系中画出抛物线m、n的草图；
（3）若将（2）中抛物线n向上平移1个单位后，又向左或向右平移若干个单位，得到顶点为N的抛物线n′，当N在抛物线m上时，问点M是否在平移后的抛物线n′上？试说明其理由．

如图，在?ABCD中，∠BAD的平分线AE交边CD于点E，∠ABC的平分线BF交边CD于点F，交AE于点G．
（1）求证：DF=EC；
（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形，并说明理由．

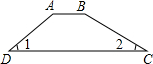随着“碰瓷”事件的频繁发生，现在老人摔倒了敢不敢扶成了一个热门话题，前段时间郑州市的一群老人针对这个现象进行了一场名为“请放心扶起我”的行为艺术，为了扩大行为艺术的影响，纠正社会风气，某老年艺术团准备举行一场义演，请你为义演舞台的选址出谋划策，如图：舞台宽度为5米，左面楼梯长3米，梯面与地面夹角∠1为40°，右面有个专供残疾演员登台用的斜坡，与地面夹角∠2为30°，且台面AB与地面DC平行，请你通过计算说明至少空地面有多宽才能搭建下这个舞台（结果保留两位小数）？（

3

≈1.732，tan40°≈0.839，sin40°≈0.643，cos40°≈0.766）

如图，抛物线经过点A（1，0），B（5，0），C（0，

10

3

）三点，设点E（x，y）是抛物线上一动点，且在x轴下方，四边形OEBF是以OB为对角线的平行四边形．

（1）求抛物线的解析式；
（2）当点E（x，y）运动时，试求平行四边形OEBF的面积S与x之间的函数关系式，并求出面积S的最大值？
（3）是否存在这样的点E，使平行四边形OEBF为正方形？若存在，求E点，F点的坐标；若不存在，请说明理由．

中央电视台有一个“购物街”节目，其中一个环节是：主持人展示三件价格不同的商品，现场的一名幸运观众将标记有数字1，2，3的三个牌子分别放在三件商品上，只要数字1，2，3分别正确放在价格高、中、低的商品上，则可同时赢得三件商品（只要有一个放错则游戏失败）．
（1）请你用列表或画树状图的方法表示出所有可能的结果；
（2）如果你随意将1，2，3分别放在三件商品上，那么你获胜的概率多大？

先化简(

a+2

a2-2a

-

8

a2-4

)÷

a-2

a+2

，然后从0，-2，1，2中选取一个你认为合适的数作为a的值代入求值．

在平面直角坐标系中，直线y=kx+2经过（-2，6），求关于x的不等式kx+2≥0的解集．

A、B、C、D四盏日光灯均处于关闭状态，它们分别由四个外形相同的开关单独控制．
（1）任意按下一个开关，恰好打开A日光灯的概率是；
（2）同时任意按下两个开关，求恰好打开A、B两盏日光灯的概率．

某校在学生中开展主题为“火灾逃生知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，分别记作A、B、C、D；并根据调查结果绘制成如图所示的扇形统计图和条形统计图（未完成），请结合图中所给信息解答下列问题：

（1）本次被调查的学生共有人；在被调查者中“基本了解”的有人；
（2）将扇形统计图和条形统计图补充完整；
（3）在“非常了解”的调查结果里，初三年级学生共有5人，其中3男2女，在这5人中，打算随机选出2位进行采访，请你用列表法或树状图的方法求出所选两位同学恰好都是男同学的概率？

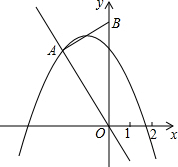在直角坐标系中，点A（-2，4）在经过原点的直线上，过A作直线OA的垂线交y轴于点B．
（1）求直线OA的解析式；
（2）求B点坐标；
（3）若抛物线y=a（x+m）²+k的顶点总是落在线段AB上，且它与x轴的一个交点落在（1，0）与（2，0）之间（包括这两点）．
当抛物线的顶点A（-2，4），与x轴交于（2，0）时，抛物线开口最大；
当抛物线的顶点B，与x轴交于（，）时，抛物线开口最小；
∴a的取值范围是： （直接写出答案）