
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 月污水处理能力(吨/月) | 200 | 160 |
查看答案和解析>>
科目: 来源: 题型:
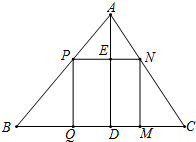 课本中有一道作业题:
课本中有一道作业题: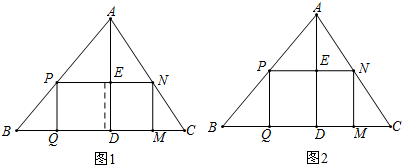
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
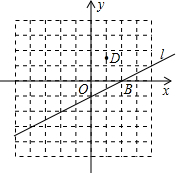 如图,已知直线l的解析式为y=
如图,已知直线l的解析式为y=| 1 |
| 2 |
| 5 |
| 4 |
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
 如图,把边长为a=2的正方形剪成四个全等的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形(要求全部用上,互不重叠,互不留隙).
如图,把边长为a=2的正方形剪成四个全等的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形(要求全部用上,互不重叠,互不留隙).
查看答案和解析>>
科目: 来源: 题型:
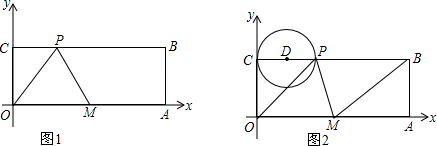
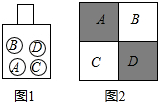 如图1,在一个不透明的袋中装有四个球,分别标有字母A、B、C、D,这些球除了所标字母外都相同,另外,有一面白色、另一面黑色、大小相同的4张正方形卡片,每张卡片上面的字母相同,分别标有A、B、C、D.最初,摆成图2的样子,A、D是黑色,B、C是白色.
如图1,在一个不透明的袋中装有四个球,分别标有字母A、B、C、D,这些球除了所标字母外都相同,另外,有一面白色、另一面黑色、大小相同的4张正方形卡片,每张卡片上面的字母相同,分别标有A、B、C、D.最初,摆成图2的样子,A、D是黑色,B、C是白色.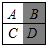 )
)查看答案和解析>>
科目: 来源: 题型:
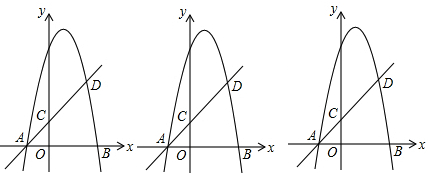
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com