阅读下面的材料:
(1)锐角三角函数概念:在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,称sinA=
,sinB=
是两个锐角∠A,∠B的“正弦”,特殊情况:直角的正弦值为1,即sin90°=1,也就是sinC=
=1.
由sinA=
,可得c=
;由sinB=
,可得c=
,
而c=
=
=,于是就有
==(2)其实,对于任意的锐角△ABC,上述结论仍然成立,即三角形各边与对角的正弦之比相等,我们称之为“正弦定理”,我们可以利用三角形面积公式证明其正确性.
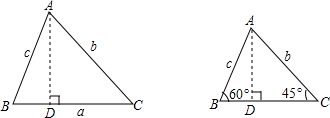
证明:如图1作AD⊥BC于D则在Rt△ABD中,sinB=
,
∴AD=c•sinB,∴S
△ABC=
a•AD=
ac•sinB,
在Rt△ACD中,sinC=
,∴AD=b•sinC.
∴S
△ABC=
a•AD=
ab•sinC.同理可得S
△ABC=
bc•sinA.
因此有S
△ABC=
ac•sinB=
ab•sinC=
bc•sinA.
也就是=ac•sinB=ab•sinC=bc•sinA.
每项都除以abc,得
==,故
==请你根据对上面材料的理解,解答下列问题:
(1)在锐角△ABC中,∠B=60°,∠C=45°,c=2,求b;
(2)求问题(1)中△ABC的面积;
(3)求sin75°的值(以上均求精确值,结果带根号的保留根号)

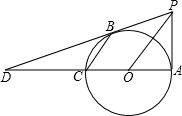 如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.
如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.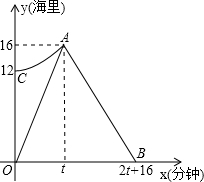 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的 有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)(如图所示)散乱地放在桌子上.
有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)(如图所示)散乱地放在桌子上.
 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AB=7,AD=4,CA=5,动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C→D→A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD交于点E,与折线A-C-B的交点为Q,设点M的运动时间为t.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AB=7,AD=4,CA=5,动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C→D→A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD交于点E,与折线A-C-B的交点为Q,设点M的运动时间为t. 阅读下面的材料:
阅读下面的材料: