如图所示，已知BE⊥AC于E，CF⊥AB于F，BE、CF相交于点D，若BF=CE．求证：（1）AD平分∠BAC；（2）AE=AF．

问题解决：
如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．
（1）如图2，固定△ABC，将△DEC绕点C旋转，当点D恰好落在AB边上时，设△BDC的面积为S₁，△AEC的面积为S₂，那么S₁与S₂的数量关系是；

（2）当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S₁与S₂的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．
（3）如图4，∠ABC=60°，点D在其角平分线上，BD=CD=6，DE∥AB交BC于点E，若点F在射线BA上，并且S_△DCF=S_△BDE，请直接写出相应的BF的长．

（1）如图①，若BC=6，AC=4，∠C=60°，求△ABC的面积S_△ABC；
（2）如图②，若BC=a，AC=b，∠C=α，求△ABC的面积S_△ABC；
（3）如图③，四边形ABCD，AC=m，BD=n，对角线AC交于O点，他们所成锐角为β，求四边形ABCD的面积S_{四边形ABCD}．

情境•观察：
将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A₁C₁D，如图1所示，将△A₁C₁D的顶点A₁与点A重合，并绕点A按逆时针方向旋转，使点D，A（A₁），B在同一条直线上，如图2所示，观察图2可知：旋转角∠CAC₁=°，与BC相等的线段是．

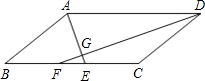已知：如图，在?ABCD中，∠BAD，∠ADC的平分线AE、DF分别与线段BC相交于点E、F，AE与DF相交于点G．
（1）求证：AE⊥DF；
（2）若AD=10，AB=6，求EF的长．

先化简，后求值：x-3（x-

1

3

y²）+6（-x+

1

3

y²），其中x=-2，y=-1．

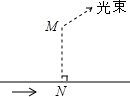一辆小车沿着水平地面上的长直轨道匀速的向右运动，有一台散发出细光束的激光器装在小转台M上，转台到轨道的距离MN=10米．转台匀速的转动，使激光器在水平面内扫描．扫描一周的时间为60秒，光束转动的方向为逆时针方向．已知当光束与MN的夹角为45°时，光束正好射到小车上，如果再经过2.5秒，光束又射到小车上，求小车的速度？（

3

≈1.73，结果保留两位有效数字）

已知A、B为数轴上的两点，A点对应的数为-20，B点对应的数为100，
（1）求AB中点C对应的数；
（2）现有个电子蚂蚁从A点出发，第一步先向左爬一个单位，第二步向右爬2个单位，第三步向左爬3个单位，第四步向右爬4个单位，按照这样的方式，需要爬多少步能爬到B点？
（3）电子蚂蚁P从点B出发，以每秒6个单位的速度向左运动，同时，电子蚂蚁Q从点A出发，以每秒4个单位的速度向右运动，两只蚂蚁在点D相遇，求C点和D点的距离．

如图，如果△A₁B₁C₁与△ABC关于y轴对称．
（1）画出△A₁B₁C₁；
（1）求点A的对应点A₁的坐标；
（2）试求△A₁B₁C₁面积．

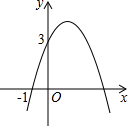已知二次函数y=-x²+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，直接写出函数值y为正数时，自变量x的取值范围；
（3）当

1

2

≤x≤2时，求y的最大值．