为了解学生参加课外阅读的喜好，某校随机抽取部分学生进行问卷调查，调查要求每人只选取一种喜欢的书籍，如果没有喜欢的书籍，则作“其它”类统计．图①与图②是整理数据后绘制的两幅不完整的统计图．

（1）被调查的学生共有人；
（2）若该校共有1200名学生，喜欢“小说”的学生估计约人；
（3）学校准备组织漫画创作培训活动．因为名额有限，李洋、张琳两人只能一人参加．老师说，现有分别写有1、2、3、4的4张卡片，先由李洋随机地抽取一张后，再由张琳随机地抽取另一张．若抽取的两张卡片上的数字之和是5的倍数则李洋参加，若抽取的两张卡片上的数字之和是3的倍数则张琳参加．问这种方法对他俩是
否公平？请用列表法或画树形图的方法分析说明．

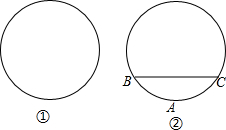某市新建了圆形文化广场，小杰和小浩准备用不同的方法测量该广场的半径．
（1）小杰先找圆心，再量半径．请你在图①中，用尺规作图的方法帮小杰找到该广场的圆心O（不写作法，保留作图痕迹）；
（2）小浩在广场边（如图②）选取A、B、C三根石柱，量得A、B之间的距离与A、C之间的距离相等，并测得BC长为240米，A到BC的距离为5米．请你帮他求出广场的半径（结果精确到米）．

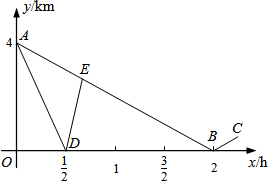
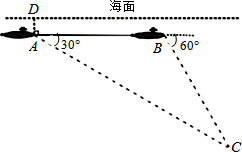如图，一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出，继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出．点C和直线AB在同一铅垂面上，求点C距离海面的深度（结果保留根号）．

阅读下面资料：
小明遇到这样一个问题：如图1，对面积为a的△ABC逐次进行以下操作：分别延长AB、BC、CA至A₁、B₁、C₁，使得A₁B=AB，B₁C=BC，C₁A=CA，顺次连接A₁、B₁、C₁，得到△A₁B₁C₁，记其面积为S₁，求S₁的值．
小明是这样思考和解决这个问题的：如图2，连接A₁C、B₁A、C₁B，因为A₁B=AB，B₁C=BC，C₁A=CA，根据等高两三角形的面积比等于底之比，所以S △A1BC=S △B1CA=S △C1AB=S_△ABC=a，由此继续推理，从而解决了这个问题．
（1）请直接写出S₁=；（用含字母a的式子表示）．
请参考小明同学思考问题的方法，解决下列问题：
（2）如图3，对面积为a的△ABC逐次进行以下操作：分别延长AB、BC、CA至A₁、B₁、C₁，使得A₁B=2AB，B₁C=2BC，C₁A=2CA，顺次连接A₁、B₁、C₁，得到△A₁B₁C₁，记其面积为S₂，求S₂的值．
（3）如图4，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，设△APE的面积为y，△BPF的面积为x，①求△APE，△BPF，△APF面积之间的关系；②求△ABC的面积．

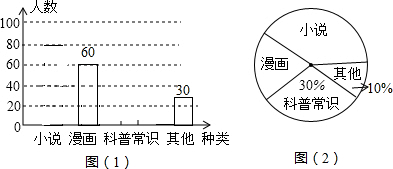
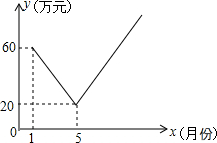保护生态环境，实行“节能减排”的理念已深入人心．我市某工厂从2014年1月开始，进行机器设备更新，产业转型换代的改造，改造期间利润明显下降，从1月份利润60万元逐月等额下降，到5月份利润为20万元；5月底改造完成，从这时起，该厂每个月的利润都比上个月增加15万元．设第x个月的利润为y（万元），函数图象如图．
（1）分别求出改造期间与改造完成后y与x的函数关系式；
（2）当月利润少于50万元时，为该厂的资金紧张期，问该厂的资金紧张期为哪几个月？

如果一个三角形的三边a，b，c能满足a²+b²=nc²（n为正整数），那么这个三角形叫做“n阶三角形”．如三边分别为1、2、

5

的三角形满足“1²+2²=1×（

5

）²，所以它是1阶三角形，但同时也满足“（

5

）²+2²=9×1²，所以它也是9阶三角形．显然，等边是三角形是2阶三角形，但2阶三角形不一定是等边三角形．
（1）在我们熟知的三角形中，何种三角形一定是3阶三角形？
（2）若三边分别是x，y，z（x＜y＜z）的直角三角形是一个2阶三角形，求x：y：z．
（3）如图1，直角△ABC是2阶三角形，AC＜BC＜AB，三条中线BD、AE、CF所构成的三角形是何种三角形？四位同学作了猜想：
A同学：是2阶三角形但不是直角三角形；  B同学：是直角三角形但不是2阶三角形；
C同学：既是2阶三角形又是直角三角形；  D同学：既不是2阶三角形也不是直角三角形．
请你判断哪位同学猜想正确，并证明你的判断．
（4）如图2，矩形OACB中，O为坐标原点，A在y轴上，B在x轴上，C点坐标是（2，1），反比例函数y=

k

x

（k＞0）的图象与直线AC、直线BC交于点E、D，若△ODE是5阶三角形，直接写出所有可能的k的值．

计算：20140+

8

-4sin45°-(

1

2

)-2．

问题情境：将一副直角三角板（Rt△ABC和Rt△DEF）按图（1）所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，∠E=30°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N．

（1）试判断线段OM与ON的数量关系，并说明理由；
（2）将图（1）中的Rt△DEF沿着射线BA的方向平移至如图（2）的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连结OM、ON．试判断线段OM、ON的数量关系与位置关系，并写出证明过程．

如图，在?ABCD中，点E、点F分别在AD、CB的延长线上，且DE=BF，连结EF分别交AB、CD于点H、点G．
求证：△EAH≌△FCG．

【实际情境】
某中学九年级学生步行到郊外春游．一班的学生组成前队，速度为4km/h，二班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时，后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12km/h．
【数学研究】
若不计队伍的长度，如图，折线A-B-C、A-D-E分别表示后队、联络员在行进过程中，离前队的路程y（km）与后队行进时间x（h）之间的部分函数图象．
（1）求线段AB对应的函数关系式；
（2）求点E的坐标，并说明它的实际意义；
（3）联络员从出发到他折返后第一次与后队相遇的过程中，当x为何值时，他离前队的路程与他离后队的路程相等？