
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
| 10 |
| 10 |
查看答案和解析>>
科目: 来源: 题型:
 如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到0.1,
如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到0.1,| 3 |
查看答案和解析>>
科目: 来源: 题型:
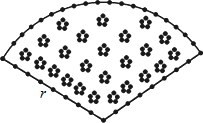 如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
 某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,如图是甲、乙两车间的距离y(千米)与乙车出发x(时)的函数的部分图象.
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,如图是甲、乙两车间的距离y(千米)与乙车出发x(时)的函数的部分图象.查看答案和解析>>
科目: 来源: 题型:
 如图,某机器人在点A待命,得到指令后从A点出发,沿着北偏东30°的方向,行了4个单位到达B点,此时观察到原点O在它的西北方向上,求A点的坐标(结果保留根号).
如图,某机器人在点A待命,得到指令后从A点出发,沿着北偏东30°的方向,行了4个单位到达B点,此时观察到原点O在它的西北方向上,求A点的坐标(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com