练习册

  • 练习册
  • 试题
    相关习题
     0  261469  261477  261483  261487  261493  261495  261499  261505  261507  261513  261519  261523  261525  261529  261535  261537  261543  261547  261549  261553  261555  261559  261561  261563  261564  261565  261567  261568  261569  261571  261573  261577  261579  261583  261585  261589  261595  261597  261603  261607  261609  261613  261619  261625  261627  261633  261637  261639  261645  261649  261655  261663  366461 

    科目： 来源： 题型：

    如图，在正方形ABCD中，点E、点F分别在边BC、DC上，BE=DF，∠EAF=60°．
    （1）若AE=2，求EC的长；
    （2）若点G在DC上，且∠AGC=120°，求证：AG=EG+FG．

    查看答案和解析>>

    科目： 来源： 题型：

    如图1，四边形ABCD、DEFG都是正方形，且C、D、E在同一条直线上，连接AE、CG．

    （1）猜想AE与CG的数量关系和位置关系，并给予说明．
    （2）把正方形ABCD绕点D旋转到如图2所示的位置，上述结论还成立吗？若成立，请给予证明；若不成立，请说明理由．

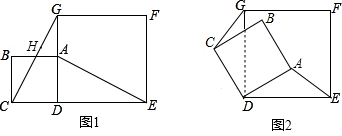
    查看答案和解析>>

    科目： 来源： 题型：

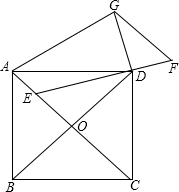    如图，正方形ABCD中，对角线AC与BD相交于O，∠ADE=15°，过D作DG⊥ED于D，且AG=AD，过G作GF∥AC交ED的延长线于F．
    （1）若ED=4
    		6
    ，求AG；
    （2）求证：2DF+ED=BD．

    查看答案和解析>>

    科目： 来源： 题型：

    一个不透明的口袋中有三个小球，上面分别标有数字2，3，4，每个小球除数字外其他都相同．小明先从袋中随机取出1个小球，记下数字后放回；再从袋中随机取出1个小球记下数字．用画树状图（或列表）的方法，求小明两次所记的数字之积大于8的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    计算：(-1)2013+(
    1
    3
    )-2-|1-
    		2
    |+(π-3.14)0+
    		8
    2
    -2sin30°    ．

    查看答案和解析>>

    科目： 来源： 题型：

    滨州市某县在全市地理学业测试前两周从10所初中随机抽取了若干名八年级学生进行地理模拟测试，并对测试成绩（x分）进行了统计，具体统计结果见下表：
    八年级地理模拟测试成绩统计表
    分数段 90＜x≤100 80＜x≤90 70＜x≤80 60＜x≤70 x≤60
    人数 60 132 328 110 120
    （1）填空：
    ①本次抽样调查共测试了
     
    名学生；
    ②参加地理会考模拟测试的学生成绩的中位数落在分数段
     
    上；
    ③若用扇形统计图表示统计结果，则分数段为90＜x≤100的人数所对应扇形的圆心角的度数为
     
    ；
    （2）该县地理成绩60分以上（含60分）的为合格，要求合格率不低于95%．现已知本次测试得60分的学生有60人，通过计算说明本次地理会考模拟测试的合格率是否达到要求？

    查看答案和解析>>

    科目： 来源： 题型：

    直角梯形ABCD中，AB∥CD，∠B=90°，AB=4，BC=4
    		3
    ，CD=8．过C点且垂直于AC的直线l以每秒2个单位的速度沿CA向A点运动；与此同时，点P、Q分别从A、B出发向C点运动，P点的运动速度为每秒2个单位，Q点的运动速度为每秒
    		3
    个单位，设P、Q点与直线l的运动时间为t．
    （1）试说明△ACD为等边三角形．
    （2）t为何值时，以P为圆心，PQ长为半径的圆与直线l相切？
    （3）求梯形ABCD与直线l在运动过程中所扫过的区域的重叠部分的面积S（用含t的代数式表示）．

    查看答案和解析>>

    科目： 来源： 题型：

    在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球．若取出的球都是红球，则小明胜出；若取出的球是一红一绿，则小颖胜出．你认为这个规则对双方公平吗？请用列表法或画树状图的方法进行分析．

    查看答案和解析>>

    科目： 来源： 题型：

    2012年3月25日浙江省环境厅第一次发布七城市PM2.5浓度数据（表一）
    2012年3月24日PM2.5监测试报数据
    城市名称 日平均浓度（微克/立方米） 分指数（IAOI）
    杭州 35 50
    宁波 49 ▲
    温州 33 48
    湖州 40 57
    嘉兴 33 48
    绍兴 44 ▲
    舟山 30 43
    （1）已知绍兴和宁波两市的分指数的和是杭州、湖州、舟山三市分指数和的
    13
    15
    ，绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10，求绍兴和宁波两市的分指数；
    （2）问上述七城市中分指数的极差是多少？位于中位数的城市是哪一个城市？
    （3）描述一组数据的离散程度，我们可以用“极差”、“方差”、“平均差”[平均差公式为T=
    1
    n
    （|x1-
    .
    x
    |+|x2-
    .
    x
    |+…+|xn-
    .
    x
    |），求杭州，温州，湖州，嘉兴，舟山五个城市中分指数的平均差．

    查看答案和解析>>

    科目： 来源： 题型：

    一家企业准备投资100万元引进一套新型设备，该设备的最大使用年限为25年．若不计维修保养费用，预计投产后每年可获毛利润65万元，从第一年到第x年的维修保养费用累计为y万元，且y=x2+x．
    （1）设w为该设备投产后第x年的累计纯利润（累计纯利润=累计毛利润-累计维修保养费用-投资），求w与x的函数关系式；
    （2）在进行预算时，若当年利润（当年利润=当年毛利润-当年维修保养费用）低于25万元，则停止使用该套设备，求第几年该企业停止使用该套设备；
    （3）在（2）的条件下，求企业使用该套设备的累计纯利润．

    查看答案和解析>>

    同步练习册答案