
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分8分)九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分8分)某种盆栽花卉每盆的盈利与每盆种植花卉的株数有关:已知每盆种植3株时,平均每株可盈利4元;若每盆多种植1株,则平均每株盈利要减少0.5元.为使每盆的盈利达到15元,则每盆应种植花卉多少株?
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分8分)如图,已知二次函数 的图象交
的图象交 轴于
轴于 、
、 两点.
两点.

(1)求线段AD的长;
(2)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x=

(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
⑴ 在如图所示的直角坐标系中,求出该抛物线的解析式;
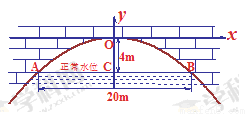
⑵ 设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下的顺利航行.
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量 是温度
是温度 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)沿海开发公司准备投资开发A、B两种新产品,通过市场调研发现:
(1)若单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;
(2)若单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
(3)根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值如下表所示:

(1)填空:yA= ;yB= ;
(2)若公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),试写出W与某种产品的投资金额x(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分12分)问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点A、B、C确定的圆为⊙O.
⑴当C、D在线段AB的同侧时,
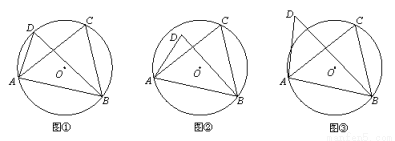
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习:(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
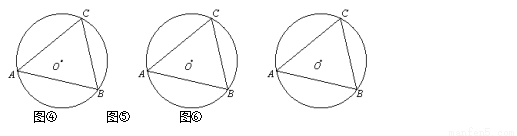
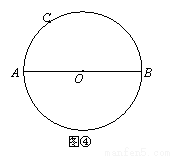
如图④,此时有 ,
如图⑤,此时有 ,
如图⑥,此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA, CB;
②在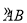 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN. 则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
查看答案和解析>>
科目: 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分12分)如图,已知抛物线 经过点B(-1,0)、C(3,0),交y轴于点A,
经过点B(-1,0)、C(3,0),交y轴于点A,

(1)求此抛物线的解析式;
(2)抛物线第一象限上有一动点M,过点M作MN⊥ 轴,垂足为N,请求出
轴,垂足为N,请求出 的最大值,及此时点M坐标;
的最大值,及此时点M坐标;
(3)抛物线顶点为K,KI⊥x轴于I点,一块三角板直角顶点P在线段KI上滑动,且一直角边过A点,另一直角边与x轴交于Q(m,0),请求出实数m的变化范围,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com