如图，△是由△经过平移后得到的，则平移的距离是（     ）

A.线段的长度            B.线段的长度     

C.线段的长度            D.线段的长度          

如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为(       )

A.10°          B.20°        C.25°          D.30°

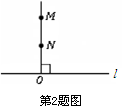
如图，已知ON⊥l,OM⊥l,所以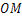与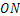重合，其理由是（    ）

A.两点确定一条直线

B.在同一平面内，经过一点有且只有一条直线与已知直线垂直

C.在同一平面内，过一点只能作一条垂线

D.垂线段最短

命题：① 邻补角互补；② 对顶角相等；③ 同旁内角互补；④ 两点之间线段最短；⑤直线都相等.其中真命题有（     ）

A. 1个         B. 2个          C. 3个        D. 4个

已知一直角边和这条直角边的对角，求作直角三角形(用尺规作图，不写作法，但要保留作图痕迹)．

 已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．

（1）直线BF垂直于直线CE于点F，交CD于点G（如图①），求证：AE=CG；

（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．

如图所示，武汉有三个车站A、B、C成三角形，一辆公共汽车从B站前往到C站．
（1）当汽车运动到点D时，刚好BD=CD，连接线段AD，AD这条线段是什么线段？这样的线段在△ABC中有几条呢？此时有面积相等的三角形吗？
（2）汽车继续向前运动，当运动到点E时，发现∠BAE=∠CAE，那么AE这条线段是什么线段呢？在△ABC中，这样的线段又有几条呢？
（3）汽车继续向前运动，当运动到点F时，发现∠AFB=∠AFC=90°，则AF是什么线段？这样的线段在△ABC中有几条？

认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题．

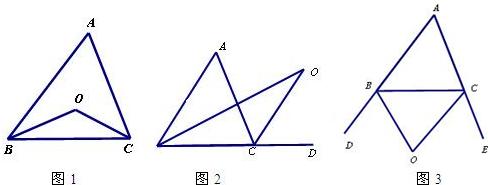
探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+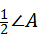，理由如下：

∵BO和CO分别是∠ABC和∠ACB的角平分线

∴

∴

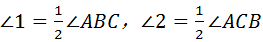
又∵∠ABC+∠ACB=180°﹣∠A

∴

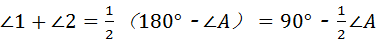
∴∠BOC=180°﹣（∠1+∠2）=180°﹣（90°﹣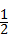∠A）

=.

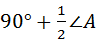探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．

探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）

结论：　     　．

如图所示，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE=AF．

求证：（1）PE=PF；2）点P在∠BAC的平分线上．

如图所示，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．