
科目: 来源: 题型:
2013年12月14日,随着嫦娥三号月球探测器缓缓降落在月球表面,中国成为继前苏联和美国后第三个实现月球软着陆的国家. 月球与地球的平均距离是384000公里. 数字384000用科学记数法表示为( )
A.3.84×105 B.38.4×104 C.0.384×106 D.3.84×106
查看答案和解析>>
科目: 来源: 题型:
定义1:在 中,若顶点
中,若顶点 ,
,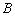 ,
, 按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
 ,
,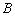 ,
, 按顺时针方向排列,则规定它的面积的相反数为
按顺时针方向排列,则规定它的面积的相反数为 的“有向面积”。“有
的“有向面积”。“有 向面积”用
向面积”用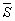 表示,
表示,


 例如图1中,
例如图1中,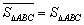 ,图2中,
,图2中,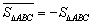 。
。
定义2:在平面内任取一个 和点
和点 (点
(点 不在
不在 的三边所在直线上),称有序数组(
的三边所在直线上),称有序数组( ,
,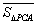 ,
, )为点
)为点 关于
关于 的“
的“ 面积坐标”,记作
面积坐标”,记作 ,例如图3中,菱形
,例如图3中,菱形 的边长为2,
的边长为2,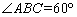 ,则
,则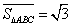 ,点
,点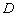 关于
关于 的“面积坐标”
的“面积坐标”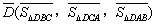 为
为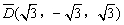 。
。
 在图3中,我们知道
在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为:
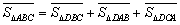 。
。
应用新知:
(1)如图4,正方形 的边长为1,则
的边长为1,则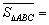 ,点
,点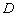 关于
关于 的“面积坐标”是 ;
的“面积坐标”是 ;
探究发现:
(2)在平面直角坐标系 中,点
中,点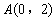 ,
,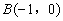 .
.
①若点 是第二象限内任意一点(不在直线
是第二象限内任意一点(不在直线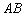 上),设点
上),设点 关于
关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究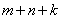 与
与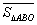 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点
是第四象限内任意一点,请直接写出点 关于
关于 的“面积坐标”(用
的“面积坐标”(用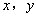 表示);
表示);
解决问题:
(3)在(2)的条件下,点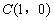 ,
, ,点
,点 在抛物线
在抛物线 上,求当
上,求当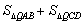 的值最小时,点
的值最小时,点 的横坐标。
的横坐标。
查看答案和解析>>
科目: 来源: 题型:
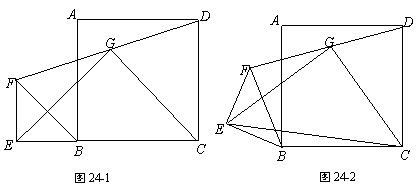
四边形 是正方形,
是正方形, 是等腰直角三角形,
是等腰直角三角形,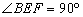 ,
,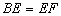 ,连接
,连接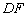 ,
,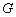 为
为
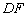 的中点,连接
的中点,连接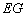 ,
,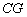 ,
,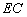 。
。
(1)如图24-1,若点 在
在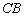 边的延长线上,
边的延长线上, 直接写出
直接写出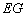 与
与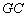 的位置关系及
的位置关系及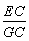 的值;
的值;
(2)将图24-1中的 绕点
绕点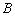 顺时针旋转至图24-2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
顺时针旋转至图24-2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)将图2 4-1中的
4-1中的 绕点
绕点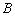 顺时针旋转
顺时针旋转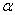 (
(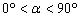 ),若
),若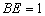 ,
,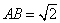 ,当
,当 ,
, ,
,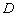 三
三
点共线时,求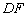 的长及
的长及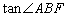 的值。
的值。
 | |||
 | |||
查看答案和解析>>
科目: 来源: 题型:
抛物线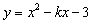 与
与 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 ,其中点
,其中点 的坐标为
的坐标为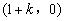 .
.
(1)求抛物线对应的函数表达式;
(2)将(1)中的抛物线沿对称轴向上 平移,使其顶点
平移,使其顶点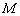 落在线段
落在线段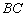 上,记该抛物线为
上,记该抛物线为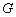 ,求抛物线
,求抛物线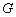
所对应的函数表达式;
(3)将线段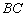 平移得到
平移得到 线段
线段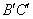 (
(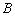 的对应点为
的对应点为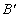 ,
, 的对应点为
的对应点为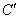 ),使其经过(2)中所得抛物线
),使其经过(2)中所得抛物线
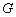 的顶点
的顶点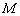 ,且与抛物线
,且与抛物线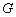 另有一个交点
另有一个交点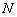 ,求点
,求点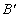 到直线
到直线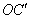 的距离
的距离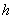 的取值范围。
的取值范围。
 |
查看答案和解析>>
科目: 来源: 题型:
阅读下列材料:
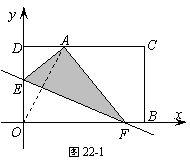
问题:在平面直角坐标系 中,一张矩形纸片
中,一张矩形纸片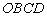 按图1所示放置。已知
按图1所示放置。已知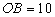 ,
,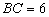 ,
,
将这张纸片折叠,使点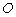 落在边
落在边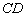 上,记作点
上,记作点 ,折痕与边
,折痕与边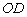 (含端点)交于点
(含端点)交于点 ,与边
,与边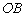 (含端
(含端
点)或其延长线交于点 ,求点
,求点 的坐标。
的坐标。
小明在解决这个问题时发现:要求点 的坐标,只要求出线段
的坐标,只要求出线段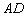 的长即可,连接
的长即可,连接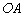 ,设折痕
,设折痕 所
所
在直线对应的函数表达式为: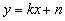
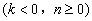 ,于是有
,于是有 ,
,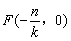 ,所以在
,所以在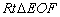
 中,得到
中,得到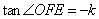 ,在
,在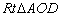 中,利用等角的三角函数值相等,就可以求出线段
中,利用等角的三角函数值相等,就可以求出线段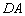 的长(如图
的长(如图
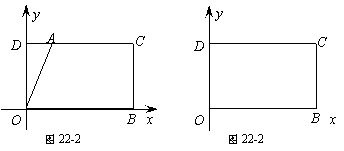 1)
1)
 |
请回答:
(1)如图1,若点 的坐标为
的坐标为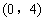 ,直接写出点
,直接写出点 的坐标;
的坐标;
(2)在图2中,已知点 落在边
落在边 上的点
上的点 处,请画出折痕所在的直线
处,请画出折痕所在的直线 (要求:尺规作图,保留作图痕迹,不写做法);
(要求:尺规作图,保留作图痕迹,不写做法);
参考小明的做法,解决以下问题:
(3)将矩形沿直线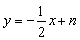 折叠,求点
折叠,求点 的坐标;
的坐标;
(4)将矩形沿直线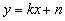 折叠,点
折叠,点 在边
在边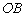 上(含端点),直接写出
上(含端点),直接写出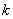 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
 以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分:
以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分:
根据以上信息,解答下列问题:
(1)2 012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元,则2012年农民人
012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元,则2012年农民人
均现金收入是 万元,请根据以上信息补全条形统计图,并标明相应的数据(结果精确到0.1);
(2)在2010—2013年这四年中,北京市城镇居民人均可支配收入和农民人均现金收入相差数额最大的年
份是 年;
(3)①2011—2013年城镇居民人均可支配收入的年平均增长率最接近 ;
A.14% B.11% C.10%  D.9%
D.9%
②若2014年城镇居民人均可支配收入按①中的年平均增长率增长,请预测2014年的城镇居民人均可
支配收入为 万元(结果精确到0.1)。
查看答案和解析>>
科目: 来源: 题型:
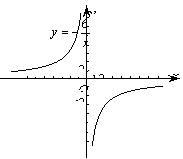
平面直角坐标系 中,一次函数
中,一次函数 和反比例函数
和反比例函数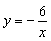 的图象都经过点
的图象都经过点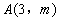 。
。
(1)求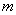 的值和一次函数的表达式;
的值和一次函数的表达式;
(2)点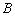 在双曲线
在双曲线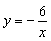 上,且位于直线
上,且位于直线 的下方,若点
的下方,若点 的横、纵坐标都是整数,直接写出点
的横、纵坐标都是整数,直接写出点 的坐标。
的坐标。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com