
科目: 来源: 题型:
如图,已知抛物线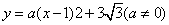 经过点
经过点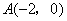 ,抛物线的顶点为
,抛物线的顶点为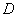 ,过
,过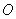 作射线
作射线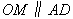 .过顶点
.过顶点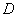 平行于
平行于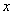 轴的直线交射线
轴的直线交射线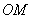 于点
于点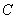 ,
,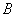 在
在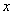 轴正半轴上,连结
轴正半轴上,连结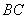 .
.
(1)求该抛物线的解析式;
(2)若动点 从点
从点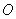 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线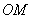 运动,设点
运动,设点 运动的时间为
运动的时间为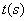 .问当
.问当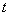 为何值时,四边形
为何值时,四边形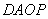 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?
(3)若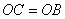 ,动点
,动点 和动点
和动点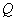 分别从点
分别从点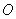 和点
和点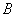 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿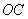 和
和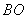 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为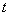
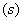 ,连接
,连接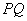 ,当
,当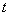 为何值时,四边形
为何值时,四边形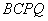 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时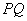 的长.
的长.
 |
查看答案和解析>>
科目: 来源: 题型:
如图,已知平面直角坐标系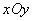 中的点
中的点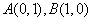 ,
,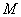 、
、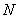 为线段
为线段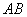 上两动点,过点
上两动点,过点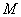 作
作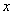 轴的平行线交
轴的平行线交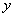 轴于点
轴于点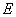 ,过点
,过点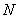 作
作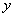 轴的平行线交
轴的平行线交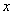 轴于点
轴于点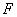 ,交直线
,交直线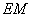 于点
于点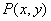 ,且
,且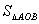 =
=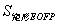 .
.
(1)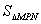
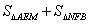 (填“>”、“=”、“<”),
(填“>”、“=”、“<”),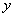 与
与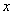 的函数关系是 (不要求写自变量的取值范围);
的函数关系是 (不要求写自变量的取值范围);
(2)当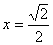 时,求
时,求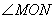 的度数;
的度数;
(3)证明: 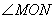 的度数为定值.
的度数为定值.
( 备用图) (备用图)
| |
查看答案和解析>>
科目: 来源: 题型:
阅读理解:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+( )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为 .
.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.

查看答案和解析>>
科目: 来源: 题型:
如图5,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若弦MN=4,求 的值以及四边形ABCD的面积.
的值以及四边形ABCD的面积.
(本题考察两直线平行,等腰三角形,锐角三角函数的求解,勾股定理,属中等难度题,考试要求b)

第20题
查看答案和解析>>
科目: 来源: 题型:
如图,已知△ABC的两边长为m、n,夹角为α ,求作一个满足下列条件的三角形EFG:含有一个内角为α;有两条边长分别为m、n,且与△ABC不全等。(要求:尺规作图,不写画法,保留作图痕迹.在图中标注m、n、 、E、F、G)
、E、F、G)

| |
查看答案和解析>>
科目: 来源: 题型:
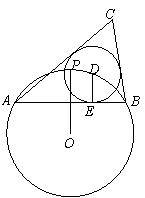
如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D
是弧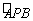 上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、
上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、
DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.①
求∠ACB的度数为 ;②记△ABC的面积为S,若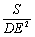 =4
=4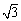 ,则⊙D
,则⊙D
的半径为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com