
科目: 来源: 题型:
已知抛物线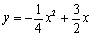 .
.
(Ⅰ)求它的对称轴与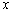 轴交点
轴交点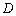 的坐标;
的坐标;
(Ⅱ)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与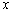 轴的交点为
轴的交点为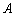 ,
,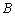 ,与
,与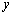 轴的交点为
轴的交点为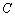 ,若
,若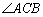 =90°,求此时抛物线的解析式;
=90°,求此时抛物线的解析式;
(Ⅲ)若点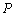 (
(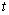 ,
,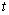 )在抛物线上,则称点
)在抛物线上,则称点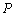 为
为 抛物线的
抛物线的 不动点.将抛物线
不动点.将抛物线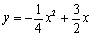 进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线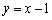 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图①,将两个完全相同的三角形 纸片
纸片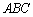 和
和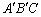 重合放置,其中
重合放置,其中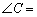 90°,
90°,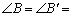 30°,
30°,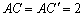 .
.
(Ⅰ)操作发现
如图②,固定△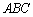 ,将△
,将△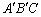 绕点
绕点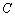 旋转,当点
旋转,当点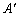 恰好落在
恰好落在 边上时,
边上时, 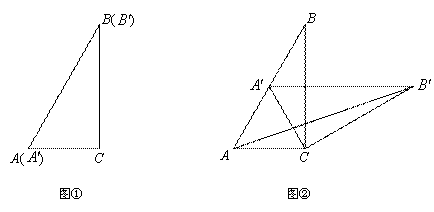
①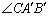 = °,旋转角α= °(0<α<90),线段
= °,旋转角α= °(0<α<90),线段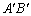 与
与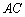 的位置关系是 ;
的位置关系是 ;
②设△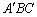 的面积为
的面积为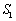 ,△
,△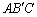 的面积为
的面积为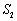 ,则
,则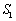 与
与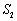 的数量关系是 ;
的数量关系是 ;
(Ⅱ)猜想论证
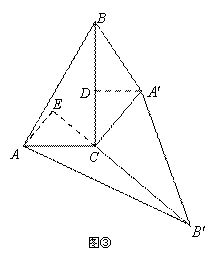
当△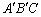 绕点
绕点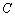 旋转到图③所示的位置时,小明猜想(Ⅰ)中
旋转到图③所示的位置时,小明猜想(Ⅰ)中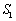 与
与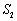 的数量关系仍然成立,并尝试分别作出了△
的数量关系仍然成立,并尝试分别作出了△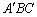 和△
和△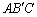 中
中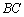 ,
,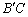 边上的高
边上的高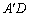 ,
,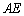 ,请你证明小明的猜想;
,请你证明小明的猜想;
(Ⅲ)拓展探究
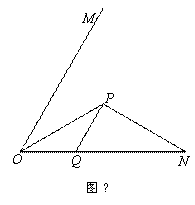
如图④,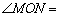 60°,
60°,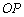 平分
平分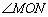 ,
,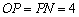 ,
,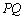 ∥
∥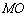 交
交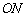 于点
于点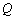 .若在射线
.若在射线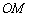 上存在点
上存在点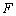 ,使
,使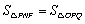 ,请直接写出相应的
,请直接写出相应的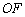 的长.
的长.
 |
 |
查看答案和解析>>
科目: 来源: 题型:
如图 将线段
将线段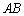 放在每个小正方形的边长为
放在每个小正方形的边长为 的网格中,点
的网格中,点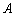 ,点
,点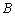 均落在格点上.
均落在格点上.
(Ⅰ)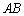 的长等于 ;
的长等于 ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺在线段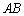 上画出点
上画出点 ,使
,使 ,并简要说明画图方法(不要求证明) .
,并简要说明画图方法(不要求证明) .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com