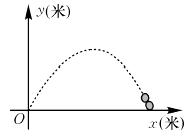
某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=-x²+4x(单位：米)的一部分，则水喷出的最大高度是(     )

  A.4米             B.3米               C.2米                D.1米

某公司销售一种进价为20元/个的计算器，其销售量y(万个)与销售价格x(元/个)的变化如下表：

价格x(元/个)…30405060…销售量y(万个)…5432…同时，销售过程中的其他开支(不含进价)总计40万元.

(1)观察并分析表中的y与x之间的对应关系，用学过的一次函数、反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式；

(2)求得该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？

(3)该公司要求净得利润不能低于40万元，请写出销售价格x(元/个)的取值范围，若还需考虑销售量尽可能大，销售价格应定为多少元？

科幻小说《实验室的故事》中，有这样一个情节：科学家把一种珍奇的植物分别放在不同温度的环境中，经过一天后，测试出这种植物高度的增长情况(如下表).

温度x/℃…-4-20244.5…植物每天高度

增长量y/mm…414949412519.75…由这些数据，科学家推测出植物每天高度增长量y是温度x的函数，且这种函数是反比例函数、一次函数和二次函数中的一种.

(1)请你选择一种适当的函数，求出它的函数关系式，并简要说明不选择另外两种函数的理由；

(2)温度为多少时，这种植物每天高度增长最大？

(3)如果实验室温度保持不变，在10天内要使该植物高度增长量的总和超过250 mm，那么实验室的温度x应该在哪个范围内选择？直接写出结果.

某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体，抽屉底面周长为180 cm，高为20 cm.请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？(材质及其厚度等暂忽略不计)

小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm²)随x(单位：cm)的变化而变化.

(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；

(2)当x是多少时，这个三角形面积S最大?最大面积是多少?

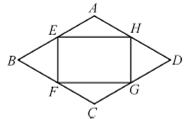
如图所示，某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上，菱形的边长AB=4米，∠ABC=60°.设AE=x米(0＜x＜4)，矩形的面积为S米².

(1)求S与x的函数关系式；

(2)学校准备在矩形内种植红色花草，四个三角形内种植黄色花草.已知红色花草的价格为20元／米²，黄色花草的价格为40元／米².当x为何值时，购买花草所需的总费用最低，并求出最低总费用(结果保留根号).

某种商品的进价为每件50元，售价为每件60元，每个月可卖出200件；如果每件商品的售价上涨1元，则每个月少卖10件(每件售价不能高于72元)，设每件商品的售价上涨x元(x为整数)，每个月的销售利润为y元.

(1)求y与x的函数关系式并直接写出自变量x的取值范围;

(2)每件商品的售价定为多少时每个月可获得最大利润?最大利润是多少?

某果园有100棵橘子树，平均每一棵树结600个橘子.根据经验估计，每多种一棵树，平均每棵树就会少结5个橘子.设果园增种x棵橘子树，果园橘子总个数为y个，则果园里增种10棵橘子树，橘子总个数最多.

某商店经营一种小商品，进价为每件20元，据市场分析，在一个月内，售价定为25元时，可卖出105件，而售价每上涨1元，就少卖5件.

(1)当售价定为每件30元时，一个月可获利多少元？

(2)当售价定为每件多少元时，一个月的获利最大？最大利润是多少元？

如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成，已知河底ED是水平的，ED=16米，AE=8米，抛物线的顶点C到ED距离是11米，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系.

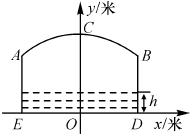
(1)求抛物线的解析式；

(2)已知从某时刻开始的40小时内，水面与河底ED的距离h(单位：米)随时间ｔ(单位：时)的变化满足函数关系

h=-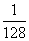(t-19)²+8(0≤t≤40)且当水面到顶点C的距离不大于5米时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？