
科目: 来源: 题型:
位似
| 定义 | 如果两个图形不仅是 |
| 性质 | 1.位似图形上任意一对对应点到位似中心的距离之比等于相似比(位似比). 2.在平面直角坐标系中,如果以原点为位似中心,相似比为k,那么位似图形上的对应点的坐标的比等于 |
查看答案和解析>>
科目: 来源: 题型:
相似三角形的性质
| 性质1 | 相似三角形的对应角⑯ ,对应边 |
| 性质2 | 相似三角形对应高的比、对应中线的比、对应角平分线的比和周长的比都等于 |
| 性质3 | 相似三角形面积的比等于相似比的 |
查看答案和解析>>
科目: 来源: 题型:
相似三角形的判定
| 判定1 | ⑩ 于三角形一 |
| 判定2 | 三边⑪ 的两个三角形相似. |
| 判定3 | 两边⑫ 且夹角⑬ 的两个三角形相似. |
| 判定4 | 两角分别⑭ 的两个三角形相似. |
| 判定5 | 满足斜边和一条直角边⑮ 的两个直角三角形相似. |
查看答案和解析>>
科目: 来源: 题型:
相似图形的有关概念
| 相似图形 | ① 相同的图形称为相似图形. |
| 相似多边形 | 两个边数相同的多边形,如果它们的角分别② ,边③ ,那么这两个多边形叫做相似多边形. |
| 相似比 | 相似多边形对应④ 的比叫做相似比. |
| 相似三角形 | 两个三角形的三个角分别⑤ ,三条边⑥ ,则这两个三角形相似.当相似比等于1时,这两个三角形⑦ . |
查看答案和解析>>
科目: 来源: 题型:
如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.



(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD=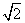 时,求线段BG的长.
时,求线段BG的长.
查看答案和解析>>
科目: 来源: 题型:
将两个斜边长相等的三角形纸片如图1放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°,把△DCE绕点C顺时针旋转15°得到△D′CE′.如图2,连接D′B,则∠E ′D′B的度数为( )
′D′B的度数为( )

A.10° B.20° C.7.5° D.15°
查看答案和解析>>
科目: 来源: 题型:
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).

(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目: 来源: 题型:
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 度;
( 2)连接AD,交OC于点E,求∠AEO的度数.
2)连接AD,交OC于点E,求∠AEO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com