
科目: 来源: 题型:
(1)如图:直线l经过正方形ABCD的顶点C,分别过点D、B作l的垂 线段DE、BF。
线段DE、BF。
求证: ≌
≌

(2)将上述的图形作为一个“基本图形”,你能否在下列的问题中构建这样的“基本图形”解决问题:
 如图正方形ABCD与正方形AEFG有共同的顶点A,连接DE、BG,过点A作直线AH⊥DE,交BG于点I,求证:I是BG的中点。
如图正方形ABCD与正方形AEFG有共同的顶点A,连接DE、BG,过点A作直线AH⊥DE,交BG于点I,求证:I是BG的中点。

(3)通过(2)的证明:我们可以发现上图中 (填“>”、“<”、或“=”)。
(填“>”、“<”、或“=”)。
并利用你的发现解决下列问题:如图:以 的各边为一边向外作正方形,各正方形的面积如图中所示,分别为9、16、25,请直接写出六边形DEFGHI的面积:_______。
的各边为一边向外作正方形,各正方形的面积如图中所示,分别为9、16、25,请直接写出六边形DEFGHI的面积:_______。

查看答案和解析>>
科目: 来源: 题型:
阅读材料:
若a,b都是非负实数,则 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵ ≥0.∴
≥0.∴ .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:
已知x>0,求函数 的最小值.
的最小值.
解: ,又
,又 ,
, 。当且仅当
。当且仅当 ,即x=2时,“=”成立.当x=2时,函数取得最小值,y最小=4.
,即x=2时,“=”成立.当x=2时,函数取得最小值,y最小=4.
问题解决:
汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油( )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目: 来源: 题型:
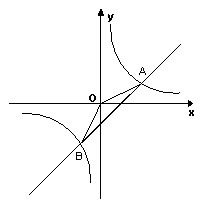
如图:已知反比例函数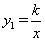 (k为常数,k≠0)的图象与一次函数
(k为常数,k≠0)的图象与一次函数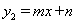 (m
(m 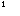 0)交于点A(2,3)点B(-1,a).
0)交于点A(2,3)点B(-1,a).
(1)求反比例函数和一次函数的关系式;
(2)利用图象直接写出当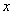 在什么范围时,
在什么范围时,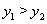 .
.
 |
查看答案和解析>>
科目: 来源: 题型:
某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
方案①:甲队单独完成此项工程刚好如期完工;
 方案②:乙队单独完成此项工程要比规定工期多用5天;
方案②:乙队单独完成此项工程要比规定工期多用5天;
方案③:若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
(1)求甲、乙两队单独完成此项工程各需多少天?
(2)如果工程不能如期完工,公司每天将损失3000元,如果你是公司经理,你觉得哪一种施工方案划算,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图, 是
是
 对角线上的两点,
对角线上的两点,
(1)给出下列三个条件:① ; ②
; ② ; ③
; ③ . 在上述三个条件中,
. 在上述三个条件中, 选择一个合适的条件说明四边形
选择一个合适的条件说明四边形 是平行四边形,则可以选择____________;
是平行四边形,则可以选择____________;
(2)选择其中的一种方案说明四边形 是平行四边形.
是平行四边形.
 |
查看答案和解析>>
科目: 来源: 题型:
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加 热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止 操作,共经历了多少时间?
操作,共经历了多少时间?
(3)该种材料温度维持在40℃以上(包括40℃)的时间有多长?

查看答案和解析>>
科目: 来源: 题型:
某中学为了解学生每天参加户外活动的情况,对部分学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)求户外活 动时间为1.5小时的人数,并补全频数分布直方图;
动时间为1.5小时的人数,并补全频数分布直方图;
(2)若该中学共有1000名学生,请估计该校每天参加户外活动的时间为1小时的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com