下列命题是真命题的是(     )

 ­A.如果两个角不相等,那么这两个角不是对顶角;     B.两互补的角一定是邻补角.

 C.如果a²=b²,那么a=b;                  D.如果两角是同位角,那么这两角一定相等

如下图，若m∥n，∠1＝105º，则∠2＝（      ）

  （A）55º  （B）60º  （C）65º（D）75º

 如下图，下列条件中，不能判断直线a//b的是（    ）

 A、∠1=∠3   B、∠2=∠3   C、∠4=∠5  D、∠2+∠4=180°

如图，OD、OE分别是与的平分线，试判断OD与OE的夹角为（    ）A 60°   B 65°     C 90°   D 80°

下列各图中，∠1与∠2是对顶角的是(       )

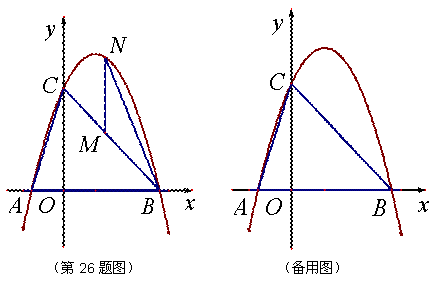
如图，已知抛物线y＝ax²＋bx＋c经过点A（-1，0）、B（3，0）、C（0，3）三点.

（1）、求抛物线相应的函数表达式;

（2）、点M是线段BC上的点（不与B、C重合），过M作MN∥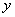轴交抛物线于N，连接NB. 若点M的横坐标为t，是否存在t，使MN的长最大？若存在，求出sin∠MBN的值；若不存在，请说明理由;

(3)、若对一切x≥0均有ax²＋bx＋c≤mx－m+13成立，求实数m的取值范围．

如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，点F为斜边AB上的一点，连接CF，CD平分∠ACF交AB于点D，点E在AC上，且有∠CFD=∠CDE.

（1）如图1，当点F为斜边AB的中点时，求CE的长；

（2）将点F从AB的中点沿AB方向向左移动到点B，其余条件不变，如图2

①求点E所经过的路径长；

②求线段DE所扫过的面积.

一辆客车从甲地出发前往乙地，平均速度(千米/小时)与所用时间（小时）的函数关系如图所示，其中.

（1）直接写出与的函数关系式；

（2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶千米，小时后两车相遇.

①分别求出两车的平均速度；

②甲、乙两地间有两个加油站A、B，它们相距千米，当客车进入B加油站时，货车恰好进入A加油站(两车加油的时间忽略不计)，求甲地与B加油站的距离.

如图，AB为⊙O的直径，弦AC=3，∠B=30°，∠ACB的平分线交⊙O于点D.

   （1）求BC、AD的长；

   （2）求图中两阴影部分的面积和.

如图，一楼房AB后有一假山，其斜坡CD坡比为1:，山坡坡面上点E处有一休息亭，测得假山坡脚C与楼房水平距离BC=6米，与亭子距离CE=20米，小丽从楼房顶测得点E的俯角为45°.

   （1）求点E距水平面BC的高度；

   （2）求楼房AB的高. （结果精确到0.1米，参考数据≈1.414，≈1.732）．