
科目: 来源: 题型:
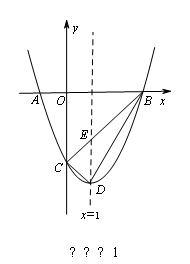
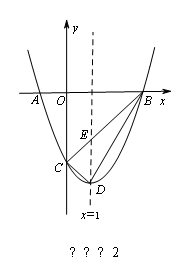
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(﹣1,0),(0,﹣3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.
(1)求抛物线的解析式并直接写出点D 的坐标;
的坐标;
(2)点P为直线x=1右方抛物线上的 一点(点P不与点B重合),记A、B、C、P四点所构成的四边形面积为
一点(点P不与点B重合),记A、B、C、P四点所构成的四边形面积为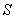 ,若
,若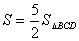 ,求点P的坐标;
,求点P的坐标;
(3)点Q是线段BD上的动点,将△DEQ沿边EQ翻折得到△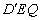 ,是否存在点Q使得△
,是否存在点Q使得△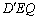 与△BEQ的重叠部分图形为直角三角形,若存在,请求出BQ的长,若不存在,请说明理由.
与△BEQ的重叠部分图形为直角三角形,若存在,请求出BQ的长,若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
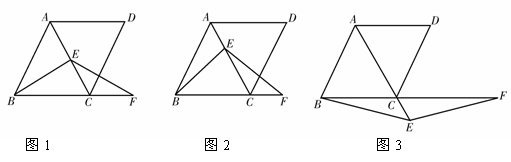 (3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
我们对多项式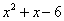 进行因式分解时,可以用待定系数法求解.例如,我们可以先设
进行因式分解时,可以用待定系数法求解.例如,我们可以先设 ,显然这是一个恒等式.根据多项式乘法将等式右边展开有:
,显然这是一个恒等式.根据多项式乘法将等式右边展开有: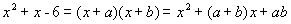
所以,根据等 式两边对应项的系数相等,可得:
式两边对应项的系数相等,可得: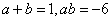 ,解得
,解得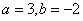 或者
或者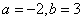 .所以
.所以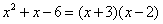 .当然这也说明多项式
.当然这也说明多项式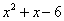 含有因式:
含有因式: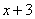 和
和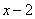 .
.
像上面这种通过利用恒等式的性质来求未知数的方法叫做待定系数法.
利用上述材料及示例解决以下问题.
(1)已知关于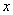 的多项式
的多项式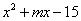 有一个因式为
有一个因式为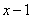 ,求
,求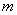 的值;
的值;
(2)已知关于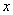 的多项式
的多项式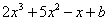 有一个因式为
有一个因式为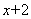 ,求
,求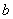 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销,购进价格为每件10元.若售价为12元/件,则可全部售出,若每涨价0.1元,销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了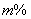 ,但售价比9月份在(1)的条件下的最高售价减少
,但售价比9月份在(1)的条件下的最高售价减少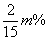 .结果10月份利润达到3388元,求
.结果10月份利润达到3388元,求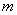 的值(
的值(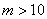 ).
).
查看答案和解析>>
科目: 来源: 题型:
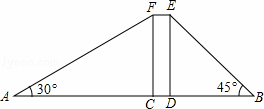
宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥却不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,你有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们来量一量吧!”君哥、宾哥在楼体两侧各选A、B两点,其中矩形CDEF表示楼体,AB=200米,CD=20米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:
(1)楼高多少米?(用含根号的式子表示)
(2)若每层楼按3米计算,你支持宾哥还是君哥的观点呢?请说明理由.(精确到0.1,参考数据: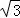 ≈1.73,
≈1.73,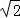 ≈1.41,
≈1.41,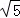 ≈2.24)
≈2.24)
查看答案和解析>>
科目: 来源: 题型:
2015年3月30日至5月11日,我校举办了以“读城 记”为主题的校读书节暨文化艺术节.为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生中随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
记”为主题的校读书节暨文化艺术节.为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生中随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
A. “寻找星主播” 校园主持人大赛 B.“育才音超”校园歌手大赛
C.阅读之星评选 D.“超级演说家”演讲比赛
(1)这次被调查的学生共有 人,请你将统计图1补充完整.
(2)在此调查中,抽到了初一(1)班3人,其中2人喜欢“育才音超”校园歌手大赛、
1人喜欢阅读之星评选.抽到了初二(5)班2人,其中1人喜欢“超级演说家”演讲比赛、1人喜欢阅读之星评选.从这5人中随机选两人,用列表或画树状图求出两人都喜欢阅读之星评选的概率.
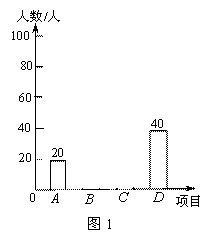 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com