
科目: 来源: 题型:
2013年,某市参加中考的学生人数为33200人.33200用科学记数法表示为
(A) 332×10 (B) 33.2×10
(B) 33.2×10
(C) 3.32×10 (D) 0.332×10
(D) 0.332×10
查看答案和解析>>
科目: 来源: 题型:
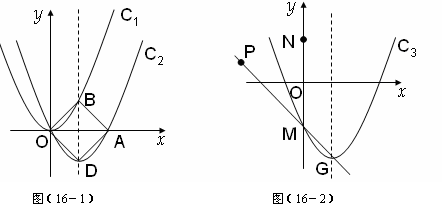
已知:抛物线C1: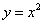 。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
(1)求抛物线C2的解析式;
(2)探究四边形ODAB的形状并证明你的结论;
(3)如图(2),将抛物线C2向m个单位下平移(m>0)得抛物线C3,C3的顶点为G,与y轴交于M。点N是M关于x轴的对称点,点P(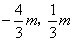 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?

查看答案和解析>>
科目: 来源: 题型:
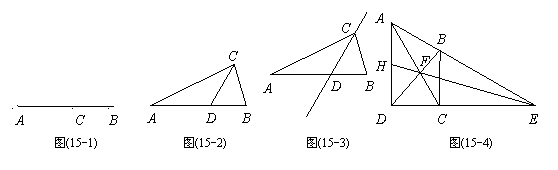
如图(15-1),点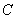 将线段
将线段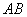 分成两部分,如果
分成两部分,如果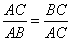 ,那么称点
,那么称点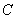 为线段
为线段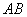 的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线
的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线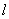 将一个面积为
将一个面积为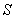 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为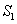 、
、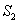 ,如果
,如果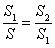 ,那么称直线
,那么称直线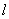 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)如图(15-2),在△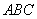 中,
中,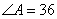 °,
°,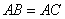 ,
, 的平分线交
的平分线交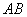 于点
于点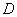 ,请问点
,请问点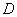 是否是
是否是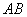 边上的黄金分割点,并证明你的结论;
边上的黄金分割点,并证明你的结论;
(2)若△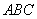 在(1)的条件下,如图(15-3),请问直线
在(1)的条件下,如图(15-3),请问直线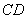 是不是△
是不是△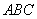 的黄金分割线,并证明你的结论;
的黄金分割线,并证明你的结论;
(3)如图(15-4),在直角梯形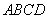 中,
中,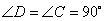 ,对角线
,对角线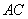 、
、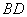 交于点
交于点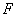 ,延长
,延长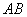 、
、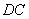 交于点
交于点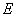 ,连接
,连接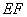 交梯形上、下底于
交梯形上、下底于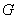 、
、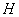 两点,请问直线
两点,请问直线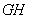 是不是直角梯形
是不是直角梯形 的黄金分割线,并证明你的结论.
的黄金分割线,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
如图,一次函数y=kx+1(k≠0)与反比例函数y= (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图 象分别交于点B,C.
象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com