
科目: 来源: 题型:
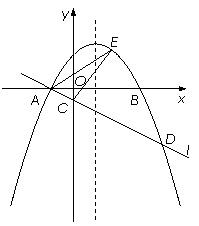
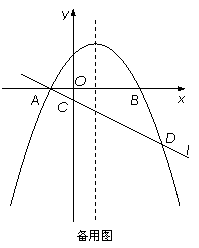
如图,在平面直角坐标系xOy中,抛物线y=ax 2-2ax-3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为 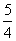 ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
 |  | ||
查看答案和解析>>
科目: 来源: 题型:
已知 分别为四边形
分别为四边形 和
和 的对角线,点
的对角线,点 在
在 内,
内, 。
。
(1)如图①,当四边形 和
和 均为正方形时,连接
均为正方形时,连接 。
。
1)求证: ∽
∽ ;2)若
;2)若 ,求
,求 的长。
的长。
(2)如图②,当四边形 和
和 均为矩形,且
均为矩形,且 时,若
时,若 ,
,
求 的值;
的值;
(3)如图③,当四边形 和
和 均为菱形,且
均为菱形,且 时,
时,
设 ,试探究
,试探究 三者之间满足的等量关系。(直接写出结果,不必写出解答过程)
三者之间满足的等量关系。(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目: 来源: 题型:
某商家预测一种应季衬衫能畅销市场,就用 元购进了一批这种衬衫,面市后果然供不应求,商家又用
元购进了一批这种衬衫,面市后果然供不应求,商家又用 元够进了第二批这种衬衫,所购数量是第一批购进量的
元够进了第二批这种衬衫,所购数量是第一批购进量的 倍,但单价贵了
倍,但单价贵了 元。
元。
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于 (不考虑其它因素),那么每件衬衫的标价至少是多少元?
(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目: 来源: 题型:
如果关于 的一元二次方程
的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是 .(写出所有正确说法的序号)
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是 .(写出所有正确说法的序号)
①方程 是倍根方程;
是倍根方程;
②若 是倍根方程,则
是倍根方程,则 ;
;
③若点 在反比例函数
在反比例函数 的图像上,则关于
的图像上,则关于 的方程
的方程 是倍根方程;
是倍根方程;
④若方程
 是倍根方程,且相异两点
是倍根方程,且相异两点 ,
, 都在抛物线
都在抛物线 上,则方程
上,则方程 的一个根为
的一个根为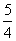 .
.
查看答案和解析>>
科目: 来源: 题型:
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2B2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.
 |
查看答案和解析>>
科目: 来源: 题型:
如图,在 中,
中, ,
, 的垂直平分线分别与
的垂直平分线分别与 ,
, 及
及 的延长线相交于点
的延长线相交于点 ,
, ,
, ,且
,且 .
. 是
是 的外接圆,
的外接圆, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 ,
, .
.
(1)求证: ;
;
(2)试判断 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若 ,求
,求 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
如图,一次函数 的图象与反比例
的图象与反比例 (
( 为常数,且
为常数,且 )的图象交于
)的图象交于 ,
, 两点.
两点.
(1)求反比例函数的表达式及点 的坐标;
的坐标;
(2)在 轴上找一点
轴上找一点 ,使
,使 的值最小,求满足条件的点
的值最小,求满足条件的点 的坐标及
的坐标及 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com